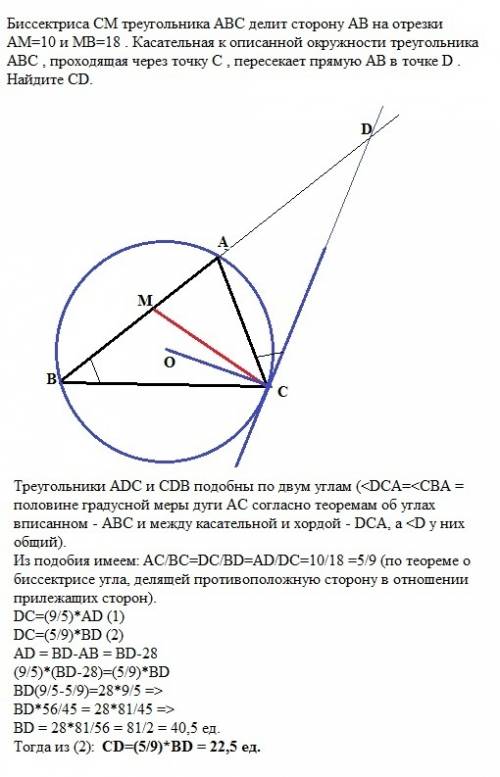
Треугольники ADC и CDB подобны по двум углам (<DCА=<CВА = половине градусной меры дуги АС согласно теоремам об углах вписанном - АВС и между касательной и хордой - DCA, а <D у них общий).
Из подобия имеем: АС/ВС=DC/BD=AD/DC=10/18 =5/9 (по теореме о биссектрисе угла, делящей противоположную сторону в отношении прилежащих сторон - АС/ВС=АМ/МВ).
Тогда из этих соотношений:
DC=(9/5)*AD (1)
DC=(5/9)*BD (2).
АВ=28 (дано), AD = BD-AB = ВD-28.
Приравняем (1) и (2):
(9/5)*(ВD-28)=(5/9)*BD
BD(9/5-5/9)=28*9/5 =>
BD*56/45 = 28*81/45 =>
BD = 28*81/56 = 81/2 = 40,5 ед.
Тогда из (2): СD=(5/9)*BD = 22,5 ед.
двух углов наверно при основании. т.е равных? трапеция ведь равнобедренная
в общем
пусть эти углы будут 1 и 2 угол
т.е угол 1 + угол 2 = 150 град
сумма углов в трапеции равна 360 градусов
360 - 150 = 210 градусов это сумма двух больших углов у другого основания
210:2=105 градусов один из больших углов( делим на два т.к трапеция равнобедренная, значит углы при основании равны)
отметь решение неверным если 150 это сумма двух углов не при основании.
удачи)))