Объяснение:
При вращении прямоугольника вокруг стороны 8 см получается цилиндр с высотой 8 см и радиусом основания 6 см.
Площадь полной поверхности цилиндра равна сумме площадей боковой поверхности и удвоенной площади основания.
Площадь боковой поверхности - произведение длины окружности основания и высоты цилиндра:
Sбок=L*Н; L=2πr=2π*6=12π, Н=8, Sбок=12π*8=96π см²;
Sосн=πr²=π*6²=36π; 2Sосн=72π см²;
Sпол.пов.=Sбок+2Sосн=96π+72π=168π см².
Объем цилиндра - произведение площади основания на высоту цилиндра.
Vцил.=Sосн*Н=36π*8=288π см³.
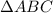
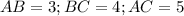
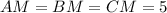
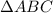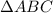. . Это - египетский прямоугольный треугольник, что подтверждается теоремой Пифагора: 
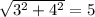. А центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Итак, радиус этой окружности равен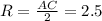 
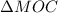. В нем 
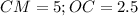. Третью сторону найдем по теореме Пифагора: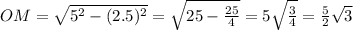
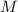до плоскости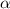 
sinB=CH/BC, но sinB=cosA=20*корень из 1/25=0,8.
Но sin^2 A+cos^2A=1, тогда sinA=корень кв. из (1-cos^2A)=корень из (1-0,64)=
=корень из 0,36=0,6