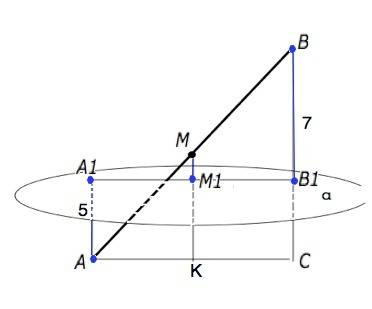
Отрезок АВ пересекает плоскость α, следовательно, т.А и т.В расположены по по разные стороны от плоскости.
Через две параллельные прямые можно провести плоскость, притом только одну. АА1 и ВВ1 лежат в одной плоскости, параллельная им ММ1 лежит в той же плоскости. Эта плоскость пересекает плоскость α по прямой А1В1.
Проведем АС║А1В1 и продолжим ММ1 до пересечения с ней в т.К, а ВВ1 - в точке С.
В параллелограмме АА1В1С стороны СВ1=АА1=5, МК параллельна им и равна 5.
В ∆ АВС прямая МК - средняя линия и равна половине ВС.
ВС=ВВ1+СВ1=12
МК=12:2=6
ММ1=МК-М1К=6-5=1 ( ед. длины)
*-градус
В треугольнике АВС угол А=30*, угол В=90*. Найдём угол С. С=180*-(30*+90*)=60*. Т.к. СМ биссектриса, то угол ВСМ=углу МСА=60*:2=30*.Рассмотрим треугольник АМС. Найдём угол АМС=180*-(30*+30*)=120*. Осталось найти АВ. Рассмотрим треугольник МВС. СМ=6см (ты написала в сообщении, хотя в условии это не сказано). По свойству прямоугольного треугольника (напротив угла в 30* лежит катет, который равен половине гипотенузы), то МВ=6:2=3см. Теперь рассмотрим треугольник АМС-вавнобедренный (т.к. угол МАС=углу АСМ=30*).АМ=МС=6см (т.к. боковые стороны равнобедренного треугольника). Теперь находим АВ. АВ=3см+6см=9см.
ответ: Угол ВСМ=30*, угол АМС=120*, АВ=9см.
сначало найдем вторую сторону прямоугольника по теореме диагонали:
25^2=24^2+x^2
x^2=625-576
x^2=49
x=7
прощадь:7*24=168