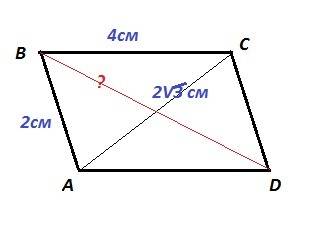
ABCD - параллелограмм. AB = 2 см, BC = 4 см, AC = 2√3 см
По теореме косинусов диагонали параллелограмма
AC² = AB² + BC² - 2 AB · BC · cos ∠B
BD² = AB² + AD² - 2 AB · AD · cos ∠A =
= AB² + AD² - 2 AB · AD · cos (180° - ∠B) =
= AB² + AD² + 2 AB · AD · cos ∠B
Так как AD = BC ⇒
BD² = AB² + BC² + 2 AB · BC · cos ∠B
Складываем почленно квадраты диагоналей.
AC² + BD² = AB² + AB² + BC² + BC²
BD² = 2 AB² + 2 BC² - AC² = 2·2² + 2·4² - (2√3)² =
= 8 + 32 - 12 = 28
BD = √28 = 2√7 см
ответ : BD = 2√7 см
Дано:
AP=PN
KP=PM
AK = 24
Доказать: ΔAPK=ΔMPN
Найти: MN
Рассмотрим Δ APK и ΔMPN, они равны, потому что AP=PN (по условию), KP=PM (по условию), ∠APK = ∠MPN (вертикальные углы), что и требовалось доказать. Так как треугольники равны, а значит они имеют равные стороны и углы, отсюда MN=AK=24
ответ: доказано; 24.
№3
Дано:
BA=DC
AD=BC
∠CAD=37
Доказать: ΔABC = ΔADC
Найти: ∠BCA
ΔABC=ΔADC, потому что AB=DC (по условию), AD=BC (по условию), AC -общая сторона, это третий признак равенства треугольников, что и требовалось доказать. В равных треугольниках против равных углов лежат равные стороны, а значит ∠BCA = ∠CAD = 37
Объяснение:
........................