Дано:
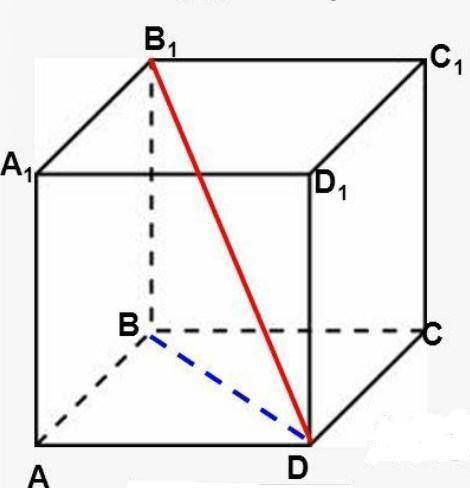
ABCDA₁B₁C₁D₁ - Куб
B₁D - диагональ куба
B₁D = d
-----------------------------------
Найти:
Sбок - ?
Применяя по теореме Пифагора к ΔABD и ΔDBB₁ последовательно имеем:
В ΔABD: BD² = AB² + AD²
В ΔDBB₁: B₁D² = BD² + BB₁² = (AB² + AD²) + BB₁²
Пусть AB = BC = CD = DA = AA₁ = BB₁ = CC₁ = DD₁ = a, следовательно:
B₁D² = (AB² + AD²) + BB₁²
d² = a² + a² + a² ⇒ d² = 3a² ⇒ d = √3a² ⇒ d = a√3 ⇒ a = d/√3
И теперь мы находим площадь боковой поверхности куба:
Sбок = 4a² = 4×(d/√3)² = 4×d²/3 = 4d²/3
ответ: Sбок = 4d²/3
P.S. Рисунок показан внизу↓
ответ:Надо доказать,что треугольники СОА и DOB равны между собой
СО=ОD по условию задачи
Угол 1 равен углу 2,тоже по условию
Угол 1 равен внутреннему углу D,a угол 2 равен внутреннему углу С,как вертикальные.
Вертикальные углы-это пары углов с общей вершиной,образованные при пересечении двух прямых так,что стороны одного угла являются продолжением сторон другого угла
По той же причине углы СОА и DOB равны между собой
Поэтому можно утверждать,что треугольники АОС и DOB равны между собой по второму признаку равенства треугольников-если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника,то такие треугольники равны между собой
Ну а если треугол Ники равны между собой то и углы А и В тоже равны между собой
Объяснение:
R=?
В прямоугольном треугольнике высота, опущенная на гипотенузу, делит его на два подобных треугольника, каждый из которых подобен исходному.
В тр-ке АВС tgA=ВС/АС=9/40=9х:40х ⇒ ВС=9х, АС=40х.
АВ=(АС²+ВС²)=√(1600х²+81х²)=41х.
Коэффициент подобия треугольников АВС и ВСР: k=BC/AB=9x/41x=9/41.
В подобных треугольниках все соответственные линейные элементы подобны, значит радиус вписанной в треугольник АВС окружности равен:
R=r/k=36·41/9=164 - это ответ.