
ответ: <1 = 110°
Объяснение: Первое выражение с учетом третьего <2 + <3 - <4 =<2 + <3 - <1 = 30 °. Это последнее выражение с учетом второго<2 + <3 - <1 =<2 + <2 - <1 = 2<2 - <1 =30 °.
С учетом второго и третьего выражений, четвертое выражение примет вид:
<1 + <2 + <3 + <4 = <1 + <2 + <2 + <1 = 2<1 + 2<2 = 360 °. Таким образом, имеем систему двух уравнений с двумя неизвестными: а)2<2 - <1 =30° и б)2<1 + 2<2 = 360°.
Из а) 2<2 = 30° + <1 Подставим значение 2<2 в б) имеем: 2<1 + 30° + <1 = 360°, или 3<1 = 360° - 30° = 330° . Отсюда <1 = 330°/3 = 110°
Дано :
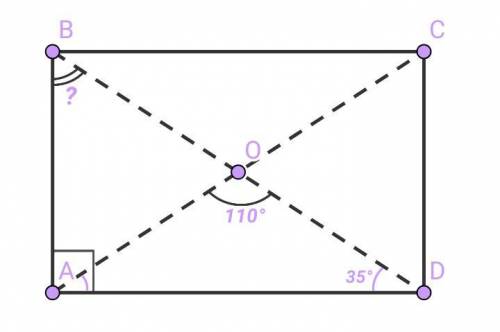
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
Задача №1 - ответ: S (4; -0,5; 2).
Задача № 2 - см. объяснение.
Задача № 3 ответ: В (0; -1; 3).
Объяснение:
Задача № 1.
Координата х = 2 + (6-2)/2 = 2+2 = 4.
Координата у = - 4 + (3-(-4))/2 = -4+3,5 = -0,5.
Координата z = 0 + (4-0)/2 = 0+ 2 = 2
ответ: S (4; -0,5; 2).
Задача № 2.
Найдём длину АВ.
Расстояние между точками A (1; 3; 2) и B (0; 2; 4) равно:
d = √((xb - xa)² + (yb - ya)² + (zb - za)²) =
= √((0 - 1)² + (2 - 3)² + (4 - 2)²) =
= √((-1)² + (-1)² + 2²) = √(1 + 1 + 4) = √6.
Найдём длину ВС.
Расстояние между точками В (0; 2; 4) и С (1; 1; 4) равно :
d = √((xс - xb)² + (yс- yb)² + (zс - zb)²) =
= √((1 - 0)² + (1 - 2)² + (4 - 4)²) =
= √(1² + (-1)² + 0²) = √(1 + 1 + 0) = √2.
Найдём длину СD.
Расстояние между точками С (1; 1; 4) и D (2; 2; 2) равно:
d = √((xd - xc)² + (yd - yc)² + (zd - zc)²) =
= √((2 - 1)² + (2 - 1)² + (2 - 4)²) =
= √(1² + 1² + (-2))² = √(1 + 1 + 4) = √6.
Найдём длину АD.
Расстояние между точками A (1; 3; 2) и D (2; 2; 2) равно:
d = √((xd - xa)² + (yd - ya)² + (zd - za)²) =
= √((2 - 1)² + (2 - 3)² + (2 - 2)²) =
= √1² + (-1)² + 0² = √1 + 1 + 0 = √2.
Таким образом, противоположные стороны четырёхугольника АВСD попарно равны:
АВ = CD = √6;
ВС = АD = √2.
Докажем, что АВ║ СD.
Для этого сравним модули разностей координат А и В с координатами С и D:
по х: |1-0| =|2-1|,
по у: |3-2| =|2-1|,
по z: |2-4| =|2-4|.
Так как разности соответствующих координат по модулю равны, то АВ║ СD.
Четырёхугольник, у которого противоположные стороны попарно равны и параллельны, является параллелограммом
Таким образом, ABCD - это параллелограмм.
Задача № 3.
К координате срединной точки С алгебраически прибавляем разность между соответствующими координатами по осям х, у, z:
xb = 1 + (1-2) = 1 - 1 = 0;
уb = 1 + (1-3) = 1 - 2 = -1;
zb = 1 + (1-(-1)) = 1+ 2 = 3.
В (0; -1; 3).