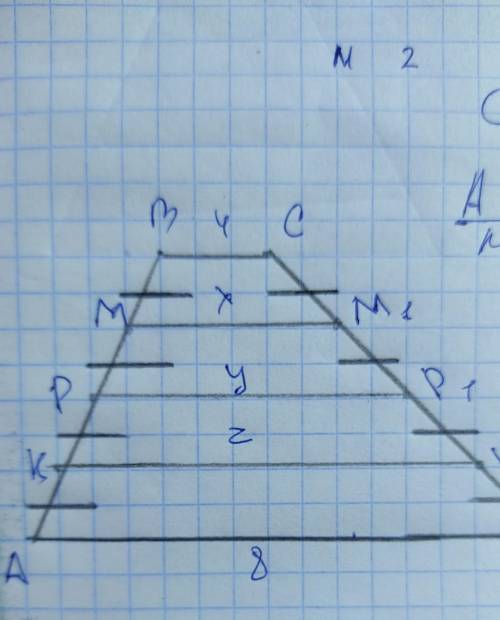
PP1(y) - средняя линия трапеции ABCD
PP1= (AD BC)/2
PP1=(8 4)/2=6(см) - y
KK1(z) - средняя линия трапеции APP1D
KK1=(AD PP1)/2
KK1=(8 6)/2=7(cм) - z
MM1(x) - средняя линия трапеции BPP1C
MM1=(BC PP1)/2
MM1=(4 6)/2=5(см) - x
1)SK=3KP=>3×1,2=3,6
KP=1,2
SP-? = KP+SK=4,8
ответ:4,8
2)PK=15
LK>PL на 3
LK-?
LK-3=PL
15-3=12 - уровнял части. Теперь LK=PL. Раз так, то делим 12 на 2=6
Теперь можно узнать LK и PM
PM=6
LK=6+3=9
ответ:9
3)MP=19
KL=11
MK-?
MK=LP
MK=(MP-KL)÷2=>(19-11)÷2=4
Oтвет:MK=4
4)NQ=28
LN=1/4NQ=>1/4×28=7
LQ-? - LN+NQ=>28+7=35
ответ:35
5)RS=12
RM÷MS=3 ÷ 9 =>RM=3;MS=9
RM -?
ответ:RM=3
6)MS=2,1
KS=0,7
KS/MK-?
MK=MS-KS=>2,1-0,7=1,4
KS/MK=0,7/1,4=0,5
ответ:KS/MK=0,5
7)AB=18
BD=4
AC/AB-?
AC=CD
AC=(AB-BD)÷2=14/2=7
AC/AB=7/18=0,4
ответ:AC/AB=0,4
8)Важная часть условия не видна
9)QM=70%SQ
SM=5,1
SQ-?
Не смог решить
10)Важная часть условия не видна
3,9,8,7,1
Вроде так, но это не точно
Два треугольника, которые можно совместить наложением, называются равными.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
z=7
y=6
x=5
Объяснение:
у меня такое же задание .__.