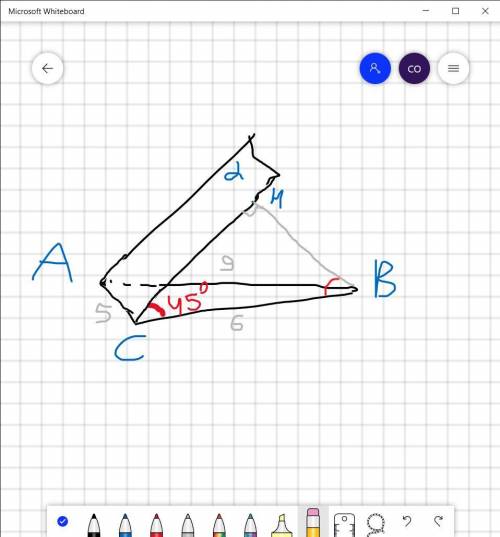
Дано: ΔABC
<(α,ABC)=45°
AB=9см ;BC = 6 см; AC = 5 см
α∩ABC =AC
BH⊥α
Знайти: BH
Розв'язання
ВС-похила до площини α, а ВН-перпендикуляр (оскільки відстань від точки до площини це перпендикуляр проведений із неї до цієї площини), тоді НС-проєкція.
Отже, проєкція похилої НС до площини трикутника ΔABC лежить на відрізку СВ => <HCB=<(α,ABC)=45°
Отримуємо прямокутний трикутник ΔВНС із прямим кутом <СНВ.
Знайдемо невідомий кут <НВС=90°-<HCB=90°-45°=45°
<HCB=<НВС, отже трикутник ΔВНС рівнобедрений і позначимо рівні сторони НС=НВ=х
За теоремою Піфагора
НС²+НВ²=СВ²
х²+х²=6²
2х²=36 | : 2
x²=18
x₁= -√18 (сторонній корень)
х₂=√18=√(9*2)=3√2 см
Відповідь: 3√2 см
(сподіваюся, що правильно)
Примем дугу ЕКН за х
Тогда дуга ЕАН=х+90
В сумме эти две дуги составляют 360 градусов.
х+х+90=360
2х=360-90
2х=270
х=135
х+90=135+90=225
Вписанный угол ЕАН опирается на дугу, равную 135 градусов. Он равен половине центрального угла, опирающегося на ту же дугу
135:2=67,5
Вписанный угол ЕКН опирается на дугу, равную 225 градусов.
Он равен половине центрального угла, опирающегося на ту же дугу и равен
225:2=112, 5
Вписанный угол ЕКА опирается на дугу 180 градусов, и равен половине центрального угла 180 градусов
180:2=90
угол ЕАН=67,5ᵒ
угол ЕКН=112, 5ᵒ
угол ЕКА=90ᵒ