Площадь прямоугольного треугольника равна 84 дм², а радиус окружности, вписанной в этот треугольник, 3см. Найти катеты треугольника.
Пусть дан треугольник АВС, угол С=90º
Точки касания вписанной окружности на АС- точка К, на ВС - точка Н, на гипотенузе АВ- точка М.
Пусть АК=х, ВН=у.
Тогда по свойству отрезков касательных из одной точки АМ=х, ВМ=у
АВ=х+у
АС=х+3, ВС=у+3
Формула радиуса вписанной окружности
r=S:p, где r -радиус, S - площадь треугольника. р- его полупериметр
р=х+у+3
3=84:(х+у+3)
х+у+3=28⇒
х+у=25
у=25-х
АВ=х+у=25 дм
АС=х+3
ВС=25-х+3=28-х
По т.Пифагора
(х+3)²+(28-х)²=625
Произведя вычисления и приведя подобные члены, получим квадратное уравнение
х²-25х+84=0
D=25²-4·84=289
Решив уравнение, найдем два корня: 21 и 4
АС=21+3=24 дм
ВС=28-21=7 дм
Кстати, длины сторон этого треугольника из Пифагоровых троек, где стороны относятся как 7:24:25

Алтын сақаның бас қаһарманы, идеялық нысанасы - халықтың арман-мұраты. Мұнда да халықтың аңсары ертегінің басты арқауы. Қазақ ертегілерінің бас қаһармандары аңшы-мерген, жауынгер-батыр, кенже бала, тазша бала, жалғыз бала және басқа әлеуметтік теңсіздіктегі бұқара өкілі. Бұлардың бәрі - халық арманынан әр кезде туған идеал кейіпкерлер. «Алтын сақадағы» бала сондай кейіпкер. Онда классикалық батырлық ертегіге тән белгілердің бәрі бар. Бала жұртта қалып қойған алтын сақасын алып келуге барып, жалмауыз кемпірге кез болған бала кемпірдің алдағанына сенбей, сақасын ат үстінен іліп алып, қаша жөнеледі. Мыстан кемпір тұра қуады. Осымен оқиға шиеленісе түседі. Бұл ертегіде де сайыста кейіпкер өз күшімен емес, керемет достарының арқасында жеңуі - батырлықтан гөрі қиял-ғажайып ертегінің заңдылықтарына жақындау.
Объяснение:
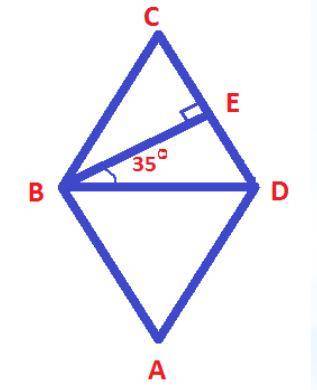
В треугольнике BDE ∡B=35°, ∡E=90°, ∡D=90-35=55°;
противоположные углы ромба равны, диагонали ромба являются биссектрисами углов, сумма углов прилежащих к одной стороне равна 180°, ⇒
в ромбе ABCD ∡D=∡B=55*2=110°, ∡A=∡C=180-110=70°.