ответ:Номер 1
Узнаем коэффициент подобия
k=AB/A1B1=28/6=3
А1С1=12:3=4 см
ВС=9•3=27 см
Номер 2
<А=<В по условию задачи
<СОА=<ВОD,как вертикальные
Треугольники
АОС и ВОD подобны по первому признаку подобия треугольников по двум углам
Узнаем коэффициент подобия
k=CO/OD=4/6=2/3
OB=5•3:2=7,5 cм
АС:ВD=2:3
S AOC/S BOD равно коэффициенту подобия в квадрате
S AOC/S BOD=4/9
Номер 3
Треугольник АВС
<С=180-(80+60)=180-140=40 градусов
Треугольник МNK
Самая большая сторона КN,значит напротив неё лежит самый большой угол
<М=80 градусов
Потом идёт сторона MN
<K=60 градусов
Самая маленькая сторона МК,соответственно -против неё находится самый маленький угол
<N=40 градусов
Объяснение:
30 см²
Объяснение:
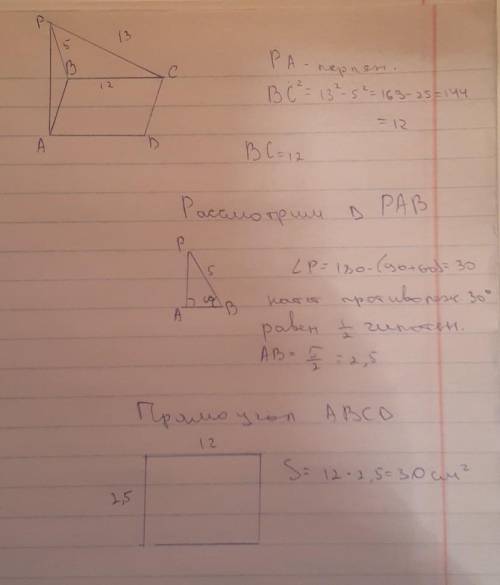
Так как в основание прямоугольник, то углы там равны все 90°
PB=5
PC=13
Если рассмотреть треугольник PBC, угол B там прямой, дальше по теореме Пифагора находим BC. ВС получилось 12
Если дальше рассмотреть треугольник АРВ там угол А=90; угол В=60°
Следовательно угол Р=30°. Далее по теореме "в прямоугольном треугольнике катет, противолежащий углу 30°, равен половине гипотенузы", в нашем случае катет АВ противолежит углу 30°, гипотенузой служит РВ, следовательно, АВ= 5:2=2,5.
Далее ищем площадь основания, в основании прямоугольник, площадь прямоугольника равна a×b. 12×2,5=30 см²
надеюсь, что объяснил доходчиво
Угол между В₁Д и пл.АВС равен углу В₁ДВ.Диагональ квадрата ВД=2√2, тогда сos<B₁DB=BD/B₁D=2√2/5, <B₁DB=arccos2√2/5.
Из ΔBB₁D : BB₁²=B₁D²-BD²= 25-8=17,BD=√17.
Диагональ прямоугольника DD₁C₁C по ттеореме Пифагора равна DC₁²=DD₁²+D₁C₁²=17+4=21, DC=√21.
Из ΔB₁DC₁ по теореме косинусов, учитывая, что B₁C₁=BC=2, получим
2²=21+25-2*√21*5*сos<B₁DC₁ , cos<B₁DC₁=42/10√21=√21/5, <B₁DC₁=arccos√21/5.