1.
Нарисовать окружность. Разделить ее радиусом на 6 частей. Две точки соединить с центром окружности. Соединить хордой концы раюиусов на окружности. Хорду обычным путем разделить на две равные части. Соединить с центром окружности.
2.
Можно построить прямой угол, проведя обычным перпендикуляр к прямой. Отложить на одной из сторон какой-то отрезок. Затем из свободного конца этого отрезка провести окружность радиусом больше того отрезка в два раза.
Точку пересечения окружности со второй стороной прямого угла соединить с концом первого отрезка. Получим треугольник с катетом длиной вдвое меньшей длины гипотенузы. Угол, лежащий против такого катета, будет равен 30 градусам.
1) 90°
2) 60°
3) 90°
Объяснение:
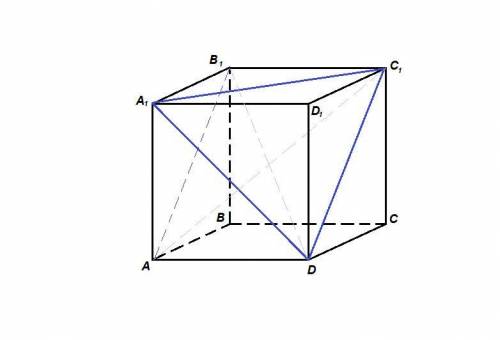
1. ВВ₁ и AD - скрещивающиеся прямые.
АА₁║ВВ₁, значит угол между ВВ₁ и AD будет равен углу между АА₁ и AD:
∠(BB₁; AD) = ∠(AA₁; AD) = 90° (смежные стороны квадрата)
2. DC₁ и DA₁.
Достроим треугольник DA₁C₁. Этот треугольник равносторонний, так как его стороны - диагонали равных квадратов. Значит,
∠(DC₁; DA₁) = ∠A₁DC₁ = 60°
3. С₁D и A₁D₁ - скрещивающиеся.
AD║A₁D₁, значит
∠(C₁D; A₁D₁) = ∠(C₁D; AD) = ∠C₁DA
AD║B₁C₁, AD = B₁C₁, значит AB₁C₁D - параллелограмм.
Диагонали куба равны, тогда AC₁ = DB₁, но это и диагонали параллелограмма AB₁C₁D, значит AB₁C₁D - прямоугольник.
∠C₁DA = 90°.
4 см, 7 см, 9 см
Объяснение:
Средняя линия треугольника равна половине основания, которому она параллельна.
8:2=4 см
14:2=7 см
18:2=9 см