Question

Точка s расположена на расстоянии 6 см от каждой из вершин прямоугольника abcd и удалена от его плоскости на 4 см. найдите стороны прямоугольника, если одна из них в 2 раза больше другой

Answer 1

SA=SB=SC=SD=6 см, SO - перпендикуляр к плоскости (АВС) (проходит через т. пересечения диагоналей прямоугольника), SO=4 см, АВ : ВС=1 : 2.

Найти: АВ=CD-?, BC=AD-?

1) Из тр-ка SOA (уг.О=90) по т. Пифагора:

$AO=\sqrt{AS^{2}-SO^{2}}=\sqrt{6^{2}-4^{2}}=\sqrt{20}=2\sqrt{5}$ (см)

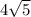2) АС=2АО=$4\sqrt{5}$ (см) (св-во диагоналей прямоуг.)

3) Пусть АВ=х (см), тогда ВС=2х (см). Из тр-ка АВС по т. Пифагора:

$AB^{2}+BC^{2}=AC^{2}$

$x^{2}+(2x)^{2}=(4\sqrt{5})^{2}$

$5x^{2}=80$

$x^{2}=16$

$x=4$ (см) - АВ=CD

4) BC=AD=2x=2*4=8 (см)

ответ: 4см; 8см.

P.S. эта задача уже была