В мастерской мастеру заказали решётку из металлических прутьев. Мастер на своём эскизе отметил только несколько величин. Вычисли, сколько метров прута нужно для изготовления заказа. AH||BG||CF||DE, DE=40 см, CF=50 см, CD=8 см, EF=10 см
2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC. . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
S=132 cм2.
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы , где - угол между сторонами a и b. Значит . . Теперь умножим эту площадь на 8. Получим .
а) Постройте плоскость, проходящую через точки K, L и М - для этого надо просто соединить эти точки.
б) Найдите угол между этой плоскостью и плоскостью основания АВС. Продлим отрезки КМ и KL до пересечения с плоскостью АВС. Для этого достаточно продлить стороны АС и АВ. Точки пресечения - это Д и Е. Примем длину отрезка АК за 1. Из треугольника АКД отрезок АД = 1 / tg 60 = 1 / √3. Аналогично АЕ = 1 / tg 45 = = 1 / 1 = 1. Угол ЕАД равен 60 градусов (по заданию). По теореме косинусов Находим гипотенузы в треугольниках АКД и АКЕ. КЕ = √(1²+1²) = √2 (острые углы по 45 градусов). Теперь определены 3 стороны в треугольнике КЕД, угол наклона которого к плоскости АВС надо найти. Для этого двугранный угол между основой и треугольником КДЕ надо рассечь плоскостью, перпендикулярной их линии пересечения ЕД. Находим высоты в треугольниках АЕД и КЕД по формуле: АЕ ДЕ АД p 2p S = 1 0.8694729 0.5773503 1.2234116 2.446823135 0.25 haе hде hад 0.5 0.57506 0.86603
КЕ ДЕ КД p 2p S = 1.4142136 0.869473 1.154701 1.719194 3.43839 0.501492 hке hде hкд 0.7092 1.15356 0.86861. Отношение высот hде и hде - это косинус искомого угла: cos α = 0.57506 / 1.15356 = 0.498510913. ответ: α = 1.048916149 радиан = 60.09846842°.
2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC.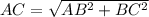
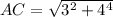 . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
. AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы , где
, где  - угол между сторонами a и b. Значит
- угол между сторонами a и b. Значит  .
. 
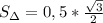 . Теперь умножим эту площадь на 8. Получим
. Теперь умножим эту площадь на 8. Получим 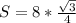
 .
.