66 см²
Объяснение:
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
⇒ ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты) ⇒
Samk/Sabm=1/2 ⇒
11/Sabm=1/2 =>
22=Sabm.
Sabk=22см²+11см²=33см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=33*2=66см²
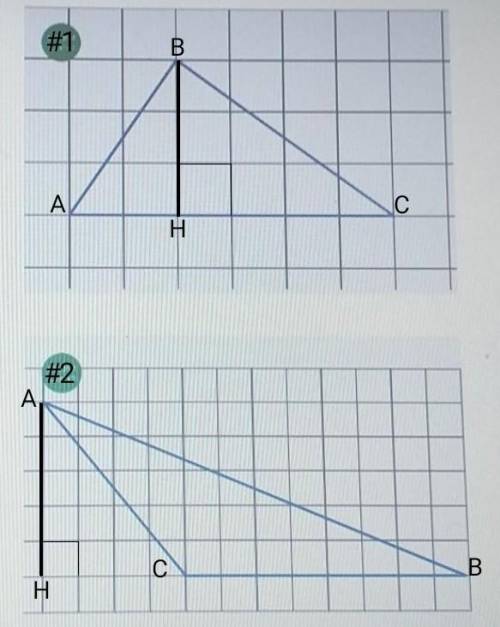
Задание #1.
Из вершины В ∆АВС на сторону АС опускаем высоту ВН.
Площадь треугольника равна половине произведения его стороны на высоту, опущенной на эту сторону.АС = 6 (ед), ВН = 3 (ед).
Тогда S∆ABC = ½×AC×BH = ½×6 (ед)×3 (ед) = 9 (ед²).
9 (ед²).
Задание #2.
Из вершины А в ∆АВС на продолжение стороны СВ опускаем высоту АН.
Площадь треугольника равна половине произведения его стороны на высоту, опущенной на эту сторону.АН = 5 (ед), СВ = 8 (ед).
Тогда S∆ABC = ½×AH×CB = ½×5 (ед)×8 (ед) = 20 (ед²).
20 (ед²).
а) Найдем для начала сторону у правильного треугольника в основании. По формуле площади правильного треугольника
Сокращаем обе части на корень из 3
По смыслу задачи сторона треугольника равна 6.
Теперь самое сложное. Придется построить высоту у треугольника в основании. Она равна по формуле площади треугольника
Теперь сократим на 3 обе части
По теореме о 3-х перпендикулярах получили прямоугольный треугольник следующего вида: первым катетом является высота треугольника в основании пирамиды. Второй катет - это его боковое ребро, перпендикулярное плоскости основания. Гипотенузой является апофема боковой грани, которая наклонена в 30 градусов к плоскости основания. Угол между гипотенузой и высотой треугольника в основании равен 30 градусам. Найдем катет, который является боковой гранью пирамиды. Он выражается через тангенс.
Теперь по теореме Пифагора найдем длины других боковых ребер пирамиды. Они равны, так как треугольники - боковые грани пирамиды равны по двум катетам. Одно ребро - общее, стороны правильного треугольника в основании пирамиды тоже равны.
Обозначим боковые ребра через l.
Длины боковых ребер равны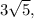
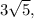 3.
3.
б) Площадь боковой поверхности равна сумме двух одинаковых прямоугольных треугольников и площади треугольника, образованного сторонами l и стороной треугольника в основании.
Площадь двух прямоугольных треугольников равна
Площадь последнего треугольника надо вычислить как половину произведения апофемы на сторону треугольника в основании
Апофема равна из треугольника в теореме о 3-х перпендикулярах. То есть теперь нужно вычислить гипотенузу этого треугольника
Теперь площадь боковой грани равна
Площадь всей боковой поверхности равна