△ABC - равнобедренный;
AB = BC;
BD = 160 (см), AC = 80 (см);
BD, AN, CM - медианы;
Найти:AN = ? (см); CM = ? (см).
Решение:"Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2 : 1, считая от вершины".
⇒ NO : AO = DO : BO = MO : CO = 1 : 2.
BO = 2/3 ⋅ BD = 2/3 ⋅ 160 = 320/3 (см).
DO = 1/3 ⋅ BD = 1/3 ⋅ 160 = 160/3 (см).
Поскольку отрезок BD - медиана ⇒ AD = DC = 80 ⋅ 1/2 = 80/2 = 40 (см).
Т.к. △ABC - равнобедренный ⇒ AO = OC (это равенство также можно обосновать тем, что прямоугольные треугольники AOD и COD равны, по двум катетам: AD = DC по свойству медианы BD, OD - общий катет).
Найдём АО и OC, по теореме Пифагора (c = √(a² + b²), где c - гипотенуза, a и b - катеты).
AO = √(DO² + AD²) = √((160/3)² + 40²) = 200/3 (см).
OC = √(DO² + DC²) = √((160/3)² + 40²) = 200/3 (см).
AO = 2/3 ⋅ AN, по свойству медиан треугольника.
Составим и решим уравнение (AN - x (см)):
2/3 ⋅ x = 200/3
x = 200/3 : 2/3
x = 200/3 ⋅ 3/2
x = 100
100 (см) - величина медианы AN.
Поскольку △ABC - равнобедренный ⇒ AN = CM = 100 (см).
ответ: 100 (см), 100 (см).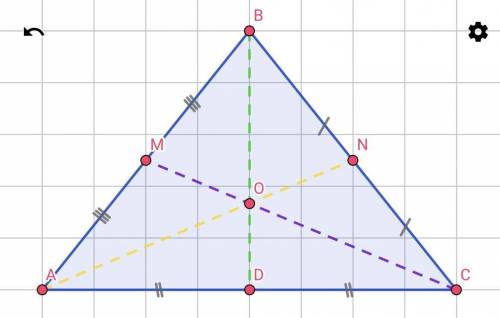
ВОТ
Объяснение:
Радиус перпендикулярен касательной в точке касания. Касательные из одной точки к окружности равны. Отрезки, соединяющие центр окружности и точку, из которой проведены касательные являются биссектрисами углов между этими касательными и углов между радиусами, проведенными к этим касательным в точки касания. Сумма острых углов прямоугольного треугольника равна 90°. Сумма всех углов с вершиной в центре окружности равна 360°. Следовательно:
<NML=2*28=56°, <MNL=2*31=62°, <NLM=180-56-62=62°, <AOM=90-28=62°, <AON=90-31=59°, <NOB=<AON=59°, <MOC=<AOM=62°, <AOC=2*<AOM=124°, <AOB=2*<AON=118°, <COB=360-124-118=118°, <COL=<BOL=<COB:2 = 59°.
Сумма острых углов прямоугольного треугольника равна 90°, значит в треугольнике АВС:
∠В = 90° - ∠А = 90° - 60° = 30°,
АС = 1/2 АВ = 1/2 · 18 = 9 см как катет, лежащий против угла в 30°.
По теореме Пифагора:
ВС = √(АВ² - АС²) = √(18² - 9²) = √(324 - 81) = √243 = 9√3 см
Площадь прямоугольного треугольника можно найти двумя
S = 1/2 AB · CH и S = 1/2 AC · BC, отсюда
AB · CH = AC · BC
CH = AC · BC / AB = 9 · 9√3 / 18 = 9√3/2 см