27,71 cм²
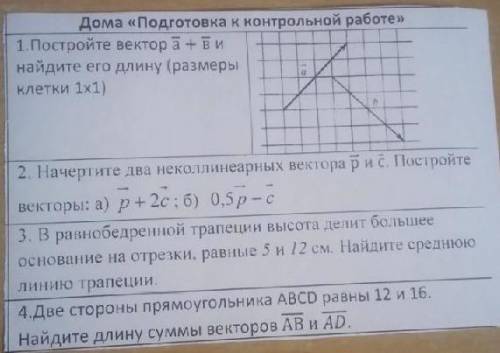
Объяснение:
1) Рассмотрим в плоскости осевого сечения прямоугольный треугольник, образованный радиусом основания, высотой и образующей.
Радиус основания и высота конуса - это катеты данного прямоугольного треугольника, а образующая - его гипотенуза.
2) В данном прямоугольном треугольнике известны 2 угла - прямой (90°) - между высотой конуса и радиусом основания и угол 60° - между образующей и радиусом основания.
Следовательно, острый угол, против которого лежит радиус основания равен:
180° (сумма внутренних углов треугольника) - 90° - 60° = 30°.
3) В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. Следовательно, радиус основания R равен:
R = 8 : 2 = 4 см.
4) Высоту рассчитаем по теореме Пифагора: катет равен корню квадратному из разности между квадратом гипотенузы и квадратом другого катета:
H = √(8² - 4²) = √ (64-16) = √ 48 = √ 16*3 = 4√3.
5) Осевое сечения конуса является треугольником, площадь которого равна половине произведения основания на высоту. Основание треугольника - это диаметр основания конуса, а высота треугольника - это высота конуса.
Диаметр основания конуса D равен:
D = 2 * R = 2 * 4 = 8 см.
6) Находим площадь осевого сечения S:
S = (D * H) : 2 = (8 * 4√3) : 2 = 16√3 cм².
Избавимся от иррациональности и рассчитаем значение площади с округлением до сотых (0,01).
16√3 ≈ 16 * 1,732 ≈ 27,71 cм²
ответ: 16√3 cм², или 27,71 cм².
ответ:tgα∗ctgα=1
а) tg \alpha =2tgα=2 ctg \alpha =1:2= 0,5ctgα=1:2=0,5
\frac{tg a+ctg a}{tg a-ctg a}= \frac{2+0,5}{2-0,5}= \frac{2,5}{1,5}= \frac{5}{3}=1 \frac{2}{3}
tga−ctga
tga+ctga
=
2−0,5
2+0,5
=
1,5
2,5
=
3
5
=1
3
2
б) \frac{sin \alpha }{cos \alpha }=2
cosα
sinα
=2 sin \alpha =2*cos \alphasinα=2∗cosα
\frac{sin a -cos a}{sin a+cos a} = \frac{2*cos a-cos a}{2*cos a+cos a}= \frac{cosa}{3cosa} = \frac{1}{3}
sina+cosa
sina−cosa
=
2∗cosa+cosa
2∗cosa−cosa
=
3cosa
cosa
=
3
1
в) \frac{2sin a+3cos a}{3sin a-7cos a} = \frac{4cos a+3cos a}{6cos a-7cos a} = \frac{7cos a}{-cos a}= \frac{7}{-1}=-7
3sina−7cosa
2sina+3cosa
=
6cosa−7cosa
4cosa+3cosa
=
−cosa
7cosa
=
−1
7
=−7
г) \frac{sin^2a+2cos^2 a}{sin^2a-2cos^2 a}= \frac{(2*cos a)^2+2cos^2 a}{(2*cos a)^2-2cos^2 a}= \frac{4cos^2 a+2cos^2 a}{4cos^2 a-2cos^2 a}= \frac{6cos^2 a}{2cos^2 a} = \frac{6}{2}=3
sin
2
a−2cos
2
a
sin
2
a+2cos
2
a
=
(2∗cosa)
2
−2cos
2
a
(2∗cosa)
2
+2cos
2
a
=
4cos
2
a−2cos
2
a
4cos
2
a+2cos
2
a
=
2cos
2
a
6cos
2
a
=
2
6
=3