В условии опечатка: надо доказать, что ΔBDC равнобедренный.
ΔBDC равнобедренный,
AD < DC.
Пошаговое объяснение:
а) Зная, что сумма углов треугольника 180°, найдем угол АВС:
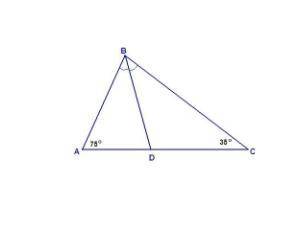
∠АВС = 180° - (∠А + ∠С) = 180° - 110° = 70°
Так как BD биссектриса угла АВС, то
∠ABD = ∠CBD = 70°/2 = 35°.
В треугольнике BDC два угла равны, значит он равнобедренный по признаку равнобедренного треугольника.
б) В треугольнике напротив меньшего угла лежит меньшая сторона.
В ΔABD AD < BD, так как AD лежит напротив угла 35°, а BD напротив угла в 75°.
Но BD = DC (доказано выше), тогда
AD < DC
надеюсь , если да то можешь пометить лучшим ответом
Объяснение:
В условии опечатка: надо доказать, что ΔBDC равнобедренный.
ΔBDC равнобедренный,
AD < DC.
Пошаговое объяснение:
а) Зная, что сумма углов треугольника 180°, найдем угол АВС:
∠АВС = 180° - (∠А + ∠С) = 180° - 110° = 70°
Так как BD биссектриса угла АВС, то
∠ABD = ∠CBD = 70°/2 = 35°.
В треугольнике BDC два угла равны, значит он равнобедренный по признаку равнобедренного треугольника.
б) В треугольнике напротив меньшего угла лежит меньшая сторона.
В ΔABD AD < BD, так как AD лежит напротив угла 35°, а BD напротив угла в 75°.
Но BD = DC (доказано выше), тогда
AD < DC
Площа бічної поверхні конуса S = πRl, де R– радіус основи конуса, l–твірна. Що б знайти радіус потрібно розглянути осьовий переріз. О – центр круга, SO – медіана, висота, бісектриса. Тоді кут 60°/2 = 30°. Розглянемо трикутник, утворений радіусом, висотою і твірною . Це прямокутний трикутник. Радіус – катет, що лежить троти кута 30°. Тому він дорівнює половині гіпотенузи – твірної. R = 15/2 = 7,5 (см); S = π·7,5·15 =112,5 π (смˆ20)
Відповідь: 112,5π смˆ2