Из большого угла проводим высоту к основанию, получаем прямоугольник и прямойгольный треугольник, находим углы в треуголнике.. основания в трапеции параллельны, поэтому проведенная высота дает прямой угол и к нижнему и к верхнему основания, тогда смотрим на больший угол равный 135, вычитаем из него прямой, получаем 45град, отсюда понимаем, что полученный треуольник прямоугольный равнобедренный, у нас известна гипотенуза, а квадрат гипотенузы, равен сумме квадратов катетов - находим катеты:
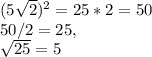
(находим квадрат гипотенузы, делим его на 2, и извлекаем корень квадратный, получаем катет)
Катет является и высотой, значит высота равна 5см, а длина прямоугольника равна 12-5=7см
Находим площадь трапеции:
-площадь прямоугольника=7*5=35
-площадь треульника=(5*5)/2=12.5
площадь трапеции=35+12.5=47,5см
AS - боковое ребро =13.
SH - апофема = 10.
АН - половина стороны (так как в правильной пирамиде боковые грани - равнобедренные треугольники), по Пифагору равна √(AS²-SH²) или
АН=√(169-100)=√69.
АВ=2√69.
АВС - правильный треугольник, в котором СН - высота, медиана и биссектриса. СН=(√3/2)*АВ (формула).
СН=(√3/2)*2√69=3√23.
НО=(1/3)*СН (свойство медианы) или
НО=√23.
Из прямоугольного треугольника SOH по Пифагору:
SO=√(SH²-HO²) или SO=√(100-23) =√77.
ответ: SO=√77.