A1.
Sшестиугольника = 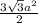
ответ: 4
A2.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
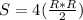
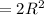
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
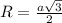
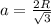
Площадь одного треугольника будет равна:
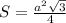
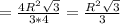
Площадь шестиугольника:
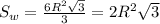
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона =  ; описанный - ΔA₁B₁C₁, сторона -
; описанный - ΔA₁B₁C₁, сторона - 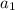
Для ΔA₁B₁C₁ радиус 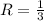 высоты
высоты 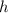
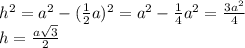
 ⇒
⇒
⇒ 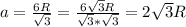
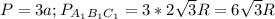
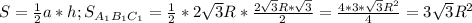
Для ΔABC радиус R = 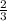 высоты
высоты 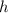 :
:
 ⇒
⇒
⇒ 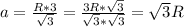
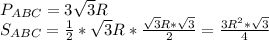
Найдем соотношение периметров и площадей:
(Сделай лучшим)
(Рисунок к задаче 8)
6) Дано:
Трикутник ABC
Кут BAZ = 150° (точка z - за межею завершенного відрізка CA)
Кут ACB = 110°
x - ?
Розв'язання:
Кут CAB, за властивістю суміжних кутів (сума суміжних кутів дорівнює 180°) дорівнює 180°-150°=30°. Сума всіх кутів трикутника дорівнює 180°. 180-110-30=40° (кут ABC). Знову використовуємо властивість суміжних кутів. 180-40=140° = x
Відповідь: x = 140°
7) Дано:
Трикутник ABC
Вертикальний кут до кута CAB = 62°
Кут ABC = 80°
x - ?
Розв'язання:
Кут, що даний і дорівнює 62° вертикальний до кута CAB, а оскільки вертикальні кути дорівнюють один одному - кут CAB дорівнює 62°. Сума всіх кутів трикутника дорівнює 180°. Кут BCA дорівнює 180°-80°-62°=38°. Оскільки вертикальні кути дорівнюють один одному то кут вертикальний до кута BCA дорівнює йому. Їх сума - 76°. Коло - 360°. x = (360-76)/2=142°
Відповідь: x = 142°
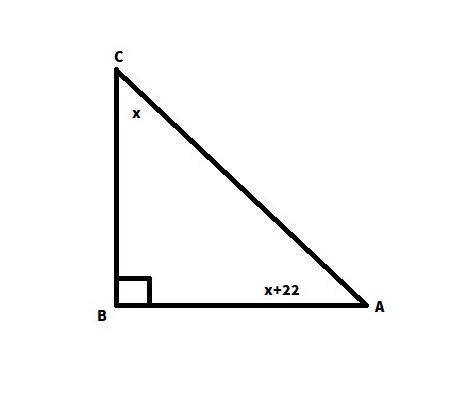
8) Дано:
Трикутник ABC (Кут B = 90°)
Кут A - Кут C = 22°
Кут C - ?
Розв'язання:
Сума всіх кутів трикутника дорівнює 180°. Сума двох гострих кутів прямокутного трикутника дорівнює 90°.
90° = x + x +22°.
68°=2x
34°=x=Кут С
Відповідь: Кут С (менший з гострих кутів трикутника) дорівнює 34°
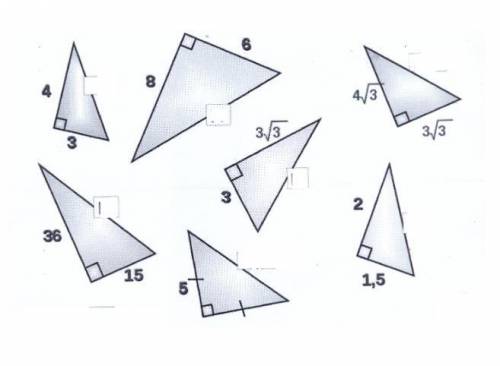
1) Это египетский треугольник,(4,3) поэтому сразу можно сказать, что гипотенуза=5
2)
3)
4)
5) треугольник прямоугольный и равнобедренный бок. ст. по 5, гип.:
6)
7)