Если вписана окружность, то суммы противоположных строн равны. Поэтому средняя линяя равна 17.
Почему суммы противоположных сторон равны? Это не только для трапеции - для любого выпуклого четырехугольника, в который можно вписать окружность. Получается это так. Точки касания делят стороны на отрезки, и отрезки, имеющие общую вершину четырехугольника, равны между собой (как касательные, проведенные к окружности из одной точки). Всего, таким образом, в общем случае есть разные 4 пары равных отрезков (сколько вершин - столько пар). Отсюда и получается, что суммы противоположных сторон - это суммы четырех таких отрезков - по одному отрезку из каждой из 4 пар.
8см
Объяснение:
Дано:
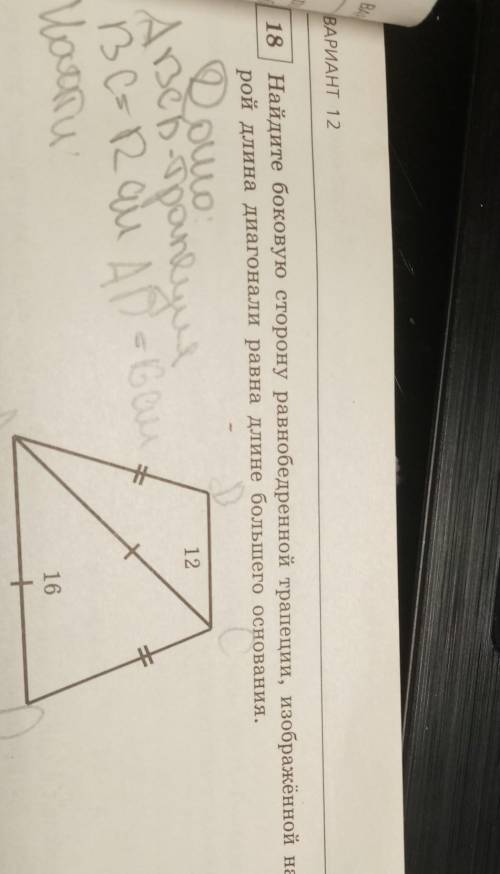
ABCD- трапеция
AD=BC
DB=DC=16см
AB=12см
AD=?
Проведём две высоты ВК и ВL
AB=KL=12см
DK=LC
LC=(DC-KL)/2=(16-12)/2=4/2=2см
DL=DC-LC=16-2=14см
Рассмотрим треугольник ∆DBL- прямоугольный.
DB- гипотенуза
DL и ВL - катеты.
По теореме Пифагора найдем ВL
ВL²=DB²-DL²=16²-14²=256-196=60
BL=√60 см
Рассмотрим треугольник ∆BLC- прямоугольный.
ВС- гипотенуза
ВL и LC - катеты.
По теореме Пифагора найдем ВС.
ВС²=BL²+LC²=(√60)²+2²=60+4=64см
BC=√64=8см
ВС=AD, по условию.
AD=8см
ВС=8см