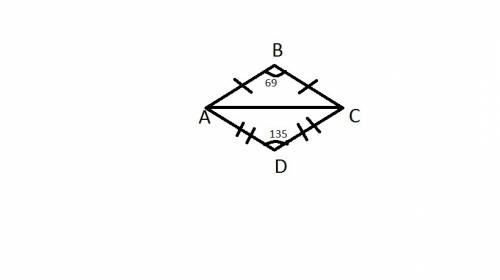
решение:дополнительное построение: проведем диоганаль АС
1) рассмотрим треугольник АВС , т.к. АВ=ВС следовательно треугольник равнобедренный а значит по свойству равнобедренного треугольника угол ВАС = ВСА а т.к. в треугольнике сумма углов = 180 градусов следовательно найдем угол А и С.
(180-69)/2=55,5 градуса
2) аналогично вычисляем угол ДАС и ДСА, получаем (180-135)/2=22,5 градуса
3) из этих вычислений мы сможем получить угол А сложив угол ВАС и ДАС 55,5+22,5=78градусов
ответ: угол А=78 градусам
Дано: ΔАВС - равнобедренный, АК = КВ = ВМ = МС (т. К и М - середины боковых сорон АВ и СВ соответственно), ВD - медиана.
Доказать: ΔBKD = ΔBMD.
Доказательство: есть два треугольника BKD и BMD, у которых сторона BD - общая. стороны KB и BM - равны, т.к. ΔABC - равнобедренный, а точки K и M - середины сторон АВ и СВ соответственно. Т.к. BD - медиана равнобедренного ΔABC, то ∠KBD = ∠DBM. Следовательно, по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны), треугольники BKD и BMD равны, т.к. KB = BM, BD - общая сторона, ∠KBD = ∠DBM.
Чтд.