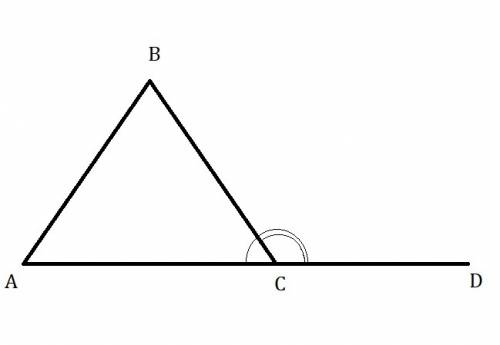
Внешним углом треугольника называется угол смежный с каким-либо углом этого треугольника.
Смотри приложение :
Дан ΔАВС .
При вершине С начертим внешний угол , обозначим его ∠ВСD.
Теорема : Внешний угол треугольника равен сумме двух углов не смежных с ним.
Дано : ΔАВС
Внутренние углы треугольника: ∠ВАС , ∠АВС , ∠ВСА
Внешний угол при вершине С: ∠ВСD
Доказать : ∠ВСD = ∠ВАС + ∠АВС
Доказательство.
1) По теореме о сумме углов треугольника :
Сумма углов (внутренних) треугольника равна 180 градусов.
∠ВАС + ∠АВС + ∠ВСА = 180°
∠ВАС + ∠АВС = 180° - ∠ ВСА
2) По свойству смежных углов:
Сумма смежных углов равна 180 градусов.
∠ВСD + ∠ BCA = 180°
∠ВСD = 180° - ∠BCA
3) ∠ВСD = ∠BAC + ∠АВС = 180° - ∠ВСА
∠ВСD = ∠BAC + ∠ABC , что и требовалось доказать...
При пересечении диагоналей образуются два подобных тр-ка, это те, в которых основания являются одними из сторон. Эти тр-ки подобны, т.к. в них равны углы, прилегающие к основаниям, как внутренние накрест лежащие и один угол - вертикальный. Коэффициент подобия 2:7.
Пусть одно основание - х, второе - у, тогдаиз подобия тр-ков следует
х:у = 2:7 (1)
и по условию
х + у = 36 (2)
Из (1) у = 3,5х (3)
подставляем (3) в (2)
х + 3,5х = 36
4,5х = 36
х = 8(см) - одно основание
у = 3,5х = 3,5 ·8 = 28(см)
ответ: основания равны 8см и 28см
Объяснение:
39:2=19.5
А=19.5