. 1. Расстояния(длины сторон) определяются, по сути по теореме Пифагора. АВ = sqrt((-4+5)^2 + (3+4)^2) = sqrt(1+49)= sqrt(50) AC = sqrt((-1+5)^2 + (1+4)^2) = sqrt(16+25) = sqrt(41) BC = sqrt((-1+4)^2 + (1-3)^2) = sqrt(9 + 4) = sqrt(13) Все стороны РАЗЛИЧНЫ, поэтому треугольник ТОЧНО НЕ РАВНОБЕДРЕННЫЙ.(Нарисуй его и ты в этом убедишься!). 2. С(-1,1) радиус = СВ = sqrt(13), поэтому уравнение искомой окружности (х+1)^2 + (y-1)^2 = 13 3. Конечно НЕТ, даже и решать не стоит, потому что СА > больше радиуса 4. По известной формуле пишем это уравнение А(-5,-4) В(-4,3) у + 4 х +5 = 3 + 4 -4 + 5 то есть у + 4 = -7х -35 у = -7х -39, ну или 7х + у + 39 = 0 Вот и всё
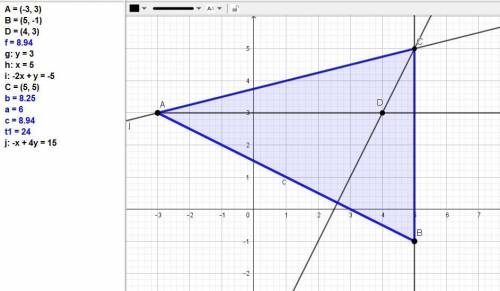
Уравнение АВ: (x-(-3))/(5-(-3) = (y-3)/(-1-3) или (x + 3)/8 = (y - 3)/(-4).
В общем виде x + 2y - 3 = 0.
Так как высота АД - горизонтальная линия, то уравнение стороны ВС:
х = 5.
В уравнении высоты СД как перпендикуляра к АВ коэффициенты А и В меняются на -В и А (скалярное произведение равно 0).
Уравнение СД: -2х + у + С = 0. Подставим координаты точки Д, через которую проходит высота: -2*4 + 1*3 + С = 0, отсюда С = 8-3 = 5.
Уравнение СД: -2х + у + 5 = 0.
Находим координаты точки С как точки пересечения стороны ВС и высоты СД:
{x = 5,
{-2х + у + 5 = 0, подставим х = 5.
-2*5 + у + 5 = 0, у = 10 - 5 = 5.
Точка С(5;5).
Уравнение АС: (x-(-3))/(5-(-3) = (y-3)/(5-3) или (x + 3)/8 = (y - 3)/2.
В общем виде x - 4y + 15 = 0.