Дано: АВСД - трапеция, ВС=12 см, АД=18 см, АС- биссектриса угла А
Найти S трапеции
1) ВС||АД, АС - секущая. Значит ∠ВСА=∠САД как накрест лежащие.
2) ∠ВАС=∠САD , потому что АС- биссектриса.
∠ВСА=∠САД как накрест лежащие. (см. пункт 1)
Отсюда следует, что ∠ВАС=∠ВСА.
3) Рассмотрим треугольнике АВС. Он равнобедренный, так ка углы при основании равны.(∠А=∠С из пункта 2). Значит АВ=ВС=12 см
4) Рассмотрим ΔАВН. ВН- высота, АВ=12 см, АН=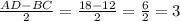
см. Этот треугольник прямоугольный, поэтому по теореме Пифагора найдём катет ВН
ВН=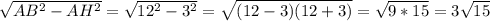 
см
5) Найдем площадь трапеции
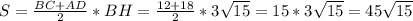см²
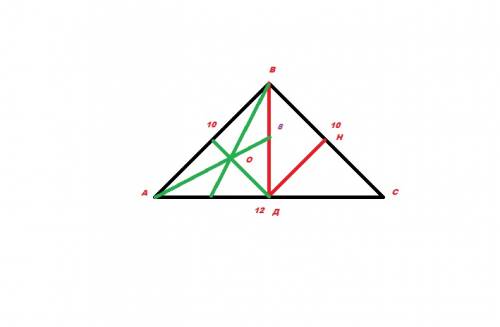
Дано:
АВ - 10
ВС - 10
АС - 10
ВД- высота
Найти:
ДН - ?
АО - ?
Р - ?
S - ?
Решение:
ВД=√(10²-(12/2)²)=√(100-36)=√64=8
периметр АВС = 10+10+12=32
площадь АВС = 10*10/2=50
периметр АВД и ВДС = 10+6+8=24
площадь АВД и ВДС = 8*6/2=24
ДМ медиана, она равна половине гипотенузы, по теореме:
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности, отсюда получам, что ДМ=10/2=5
ДО можно вычислить по формуле: r=(a*b)/(a+b+c)=8*6/24=2.
DH найдём по формуле h=ab/c=8*6/10=4.8
1. В прямоугольном треугольнике катет лежащий против угла в 30 градусов равен половине гипотенузы BC равно 4 см