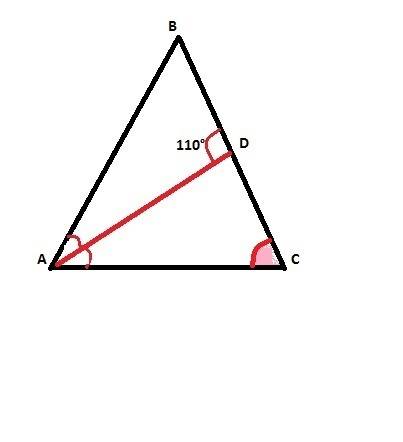
Дано: ΔАВС, DE - средняя линия.
11) Scde = 96
12) Scde = 20
13) Scde = 35
16) Scde = 21.
Найти: Sabc.
Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
∠CDE = ∠CAB как соответственные при пересечении параллельных прямых DE и АВ секущей СА,
угол при вершине С общий для треугольников CDE и CAB, значит
ΔCDE подобен ΔCAB по двум углам.
k = CD : CA = 1/2
Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
Scde : Sabc = k² = (1/2)² = 1/4
Sabc = 4 · Scde
11) Sabc = 4 · 96 = 384
12) Sabc = 4 · 20 = 80
13) Sabc = 4 · 35 = 140
16) Sabc = 4 · 21 = 84.
Основания, наверное, AD и BC.
Площадь треуг.ABD равна S(ABD)=1/2* AD*h, где h- высота, опущенная из точки В на AD.
S(BDC)=1/2*BC*h,где h- высота трапеции,опущенная из точки D на BC.
Обозначим высоту ΔВОС через х, тогда высота ΔAОD будет (h-x).
S(ABD):S(BDC)=(1/2*AD*h):(1/2*BC*h)=AD/BC
S(ABD):S(BDC)=9:4=AD*(h-x) :BC*x ⇒ AD/BC=9x/4(h-x)
Но ΔAOD подобен ΔBOC , поэтому AD:BC=(h-x):x. Подставим в предыдущее соотношение:AD/BC=(9*BC)/(4*AD) ⇒ AD²/BC²=9/4 ⇒ AD/BC=3/2 ⇒ S(ABD):S(BDC)=3:2