1. Он прямоугольный, т.к. квадрат одной стороны равен сумме квадратов двух других.
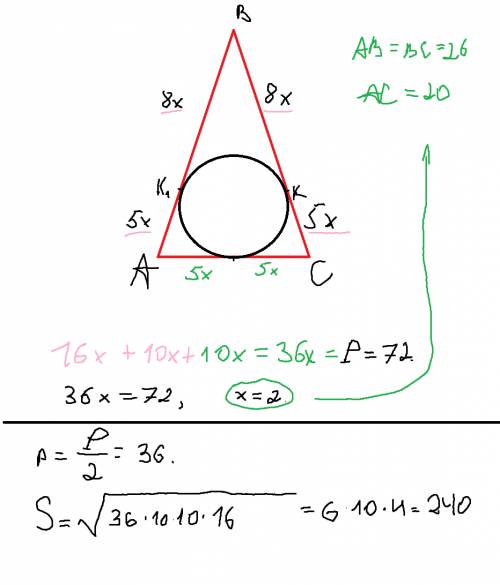
2. Т.к. АВС равнобедренный, то, очевидно, точка касания с другим бедром - АВ - будет делить его в таком же отношении. Далее вводим коэффициент пропорциональности х.
Теперь смотрим на основание. По теореме об окружности, вписанной в угол, мы имеем, что расстояния от вершины угла (в данном случае точки А и С со вписанной окружностью) до точек касания равны. Так, получается, что основание равно 10х.
Складываем все стороны и вычисляем х через известный периметр. Из этого находим все стороны треугольника.
Если все стороны известны, то площадь можно найти по формуле Герона.
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.