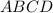, боковые стороны которые 
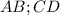, обозначим их как соответственно 
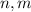, пусть 
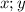отрезки другой диагонали , и пусть 
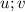отрезки диагонали 
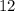,из подобия треугольников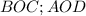 
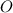пересечения диагоналей , получим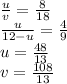 
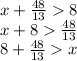получим что ![x \in [5;11]](/tpl/images/0375/3202/02960.png)
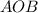
![n \in [5;8]](/tpl/images/0375/3202/42658.png)
, то есть всего 4 значения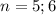 
не подходит так как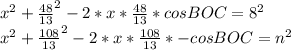 
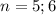
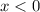что не подходит , тогда 
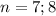, проверим оба , при 
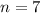, другая часть диагонали не будет входит в отрезок , по тем же самым причинами что сказано вверху, только для треугольников 
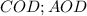, подходит 
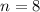при этом 
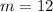что верно по неравенству треугольников 
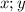, по теореме Пифагора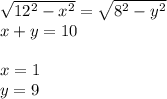 
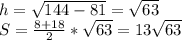
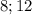
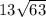
катеты этого тр-ка: АВ = АС·sin30 = 18·0.5 = 9; ВC = AC·cos30 = 18 ·0.5√3 = 9√3
Точка М середина ребраВВ1, противоположного гипотенузе АС, МВ = 4,5.
Сечение,проходящее через точки А, С. М является тр-ком с основанием Ас и высотой МД, пока неизвестной.
Проекцией МД на плоскость основания является отрезок ВД перпендикулярный АС.
В тр-ке ВСД угол Д прямой,, угол С = 30гр, тогда ВД = ВС·sin30 = 9√3 · 0,5 = 4,5√3
В тр-ке ВМД МД - гипотенуза, ВМ = 4,5 и ВД = 4,5√3 найдём МД = √(ВМ² + ВД²) =
= √(4,5² +(4,5√3)²) = 9
Площадь тр-ка АСМ S = 0.5АС·МД = 0,5·18·9 = 81
ответ: 81