Объяснение:
1)АМ - гипотеза, ВМ-катет против угла 30*,тогда
ВМ=1/2 ВМ=26:2=13
2)<А=90-60=30*,тогда ВМ-катет против угла 30*,ВМ=30:2=15
5)∆АВС - равносторонний, все углы равны и высота является биссектрисой, <МАВ=30*
Расстояние от М до АВ - это перпендикуляр МК к стороне АВ и в ∆МКА МК является катетом против угла 30* и МК=МА:2=8:2=4
6) кратчайшее расстояние от М до АВ - это высота из вершины М.
∆АВМ прямоугольный, равнобедренный и высота МН является медианой. Тогда по свойству медианы прямоугольного треугольника МН=8:2=4
По т.Пифагора найдём гипотенузу.
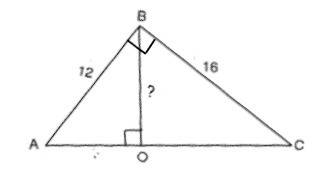
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
квартет це звуть квартет