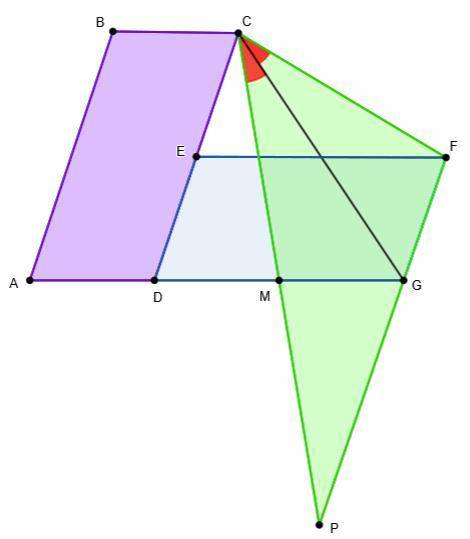
AB=CD - по свойству параллелограмма ABCD
AB=2*DE=CD ⇒ точка Е - середина CD
CE=ED=AD=DM=MG ⇒ CD=DG
четыр-ник ECFG - параллелограмм
CE || FG, так как ED || FG - по свойству параллелограмма EDGFCE=FG, так как ED=FG - по свойству параллелограмма EDGFЗначит, СF=EG - по свойству параллелограмма ECFG
ΔCDG - равнобедренный ⇒ CM=GE - медианы, проведенные к боковым сторонам равнобедренного треугольника
Поэтому CF=CM
Продолжим прямую СM до пересечения с прямой FG в точке P
ΔCMD=ΔPMG - по стороне и двум прилежащим к ней углам
DM=MG - по условию∠CMD=∠PMG - как вертикальные углы∠CDG=∠PGD - как накрест лежащие углы при CD || PG и секущей DGЗначит, CM=MP, CD=PG
Рассмотрим ΔСPF: CF=CM=MP, PG=2*FG
FG/PG=1/2 и CF/CP=1/2
Известное свойство биссектрисы:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам
Это свойство работает и в обратную сторону.
Следовательно, CG - биссектриса угла MCF, ч.т.д.
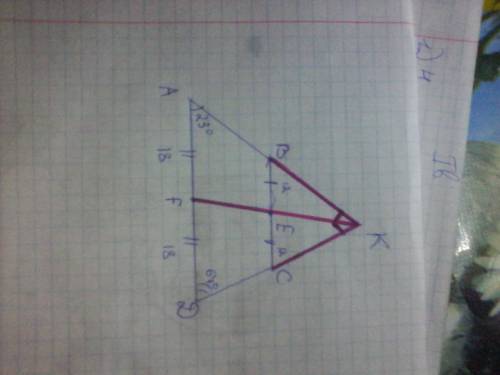
Sосн=54√3см²
Sбок=324см²
Sпол=108√3+324 см²
V=486см³
Объяснение:
Основание состоит из 6 равносторонних треугольников.
Найдем площадь одног равностороннего треугольника.
S=a²√3/4, где а - сторона треугольника.
S=6²√3/4=36√3/4=9√3 см² площадь треугольника.
В основании 6 таких равновеликих треугольников
Sосн=6*9√3=54√3 см² площадь основания.
Росн=6*6=36см периметр основания.
Sбок=Росн*h, где h- высота призмы.
Sбок=36*9=324см² площадь боковой поверхности призмы.
Sпол=2Sосн+Sбок=2*54√3+324=
=108√3+324 см² площадь полной поверхности призмы.
V=Socн*h=54√3*9=486 см³ объем призмы.