Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.
Угол между боковой гранью и основанием пирамиды - угол между двумя перпендикулярными лучами, проведенными в плоскости грани и основания к одной точке к линии их пересечения.
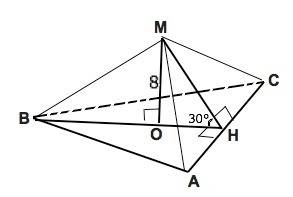
Высота основания АН и высота МН боковой грани пирамиды МАВС перпендикулярны ребру АВ в его середине Н.
Высота пирамиды МО, часть высоты основания ОН и апофема МН образуют прямоугольный треугольник МОН, в котором высота пирамиды – катет, который противолежит углу 30°, а апофема является гипотенузой.
Гипотенуза вдвое больше катета, котороый лежит против угла 30°.
Следовательно, апофема, являясь гипотенузой ∆ МОН, равна 2•8=16 м.
чтобы доказать,что ,нужно чтобы АВ было параллельло и равно CD,и то же самое со сторонами AD и ВС.
АВ имеет координаты (3-1; 5-1)=(2;4); длина АВ=√2²+4²=√20
DC (9-7; 5-1)=(2;4); DC=√2²+4²=√20, следовательно они равны.
AD (7-1; 5-1)=(6;4); AD=√6²+4²=√40
BC (9-3; 1-5) = (6;-4); ВС=√6²+(-4)²=√40,следовательно они тоже равны.
из всего вышесказанного следует,что ABCD-параллелограмм.
Диагонали так же искать через координаты:
АС (8;0); АС=√64=8
ВD(4;0); ВD=√16=4
Объяснение:
держи, надеюсь на лучший ответ