Дано: Решение:
∠AOB = 1/9 ∠BOC ∠AOB = ∠COD и ∠BOC = ∠DOA как
вертикальные углы при пересекающихся
Найти: ∠AOB; ∠BOC; прямых.
∠COD; ∠DOA Тогда: ∠AOB = ∠COD = х
∠BOC = ∠DOA = 9х
Сумма всех 4-х углов - 360°
2*(х + 9х) = 360
10х = 180
х = 18 9х = 162
∠AOB = ∠COD = 18°
∠BOC = ∠DOA = 162°
Может так ?
Объяснение:
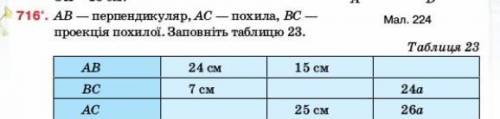
Теорема Пифагора
АВ и ВС - катеты
АС- гипотенуза.
1)
√(24²+7²)=√(576+49)=√625=25см
2)
√(25²-15²)=√(625-225)=√400=20см
3)
√((26а)²-(24а²))=√(676а²-576а²)=
=√(100а²)=10а