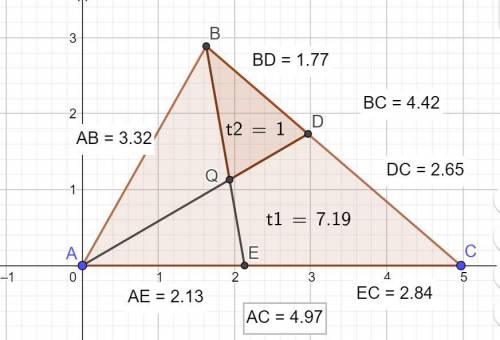
Из заданного соотношения длин сторон треугольника АВС имеем:
АВ = 1, АС = (3/2)АВ, ВС = (4/3)АВ.
Приводим к общему знаменателю и представляем длины сторон подобного треугольника в целом виде: А1В1 = 6, А1С1 = 9, В1С1 = 8.
Находим углы этого (они же и у заданного) треугольника по теореме косинусов : cosα = (b²+c²−a²)/2bc.
Подставив данные длин сторон треугольника А1В1С1, находим:
cos A = 0,490741,
cos B = 0,1979167,
cos C = 0,756944.
Соответственно углы равны:
A = 1,057857 радиан или 60,61072 градусов,
B = 1,371564 78,584842,
C = 0,712172 40,804438.
Отсюда находим угол Q1D1B1 по сумме углов смежного треугольника: ∠Q1D1B1 = (1/2)∠А + ∠С = 71,109798 градуса.
Теперь переходим к длинам треугольника Q1D1B1.
Длина B1D1 по свойству биссектрисы р = ((ас)/(b + c)) равна:
B1D1 = p = (8*6)/(9 + 6) = 48/15 = 16/5 = 3,2.
Отрезок С1D1 = q = 8 - 3,2 = 4,8.
Находим длину биссектрисы А1D1:
A1D1 = √(bc - pq) = √(9*6 - 3,2*4,8) = √38,64 ≈ 6,216108.
Биссектриса А1D1 делится точкой пересечения с биссектрисой В1Е1 в отношении (b + c)/a. Отсюда находим длину Q1D1.
Q1D1 = A1D1*(a/(a + b +c)) = 6,216108*(8/23) = 2,162125.
Теперь можно определить площадь подобного треугольника Q1D1B1 по двум сторонам и углу между ними.
S(Q1B1D1) = (1/2)*2,162125*3,2*sin71,109798° = 3,273079.
Находим коэффициент"к" пропорциональности треугольников QBD и Q1B1D1:
к =√(S(QBD)/S(Q1B1D1)) = √(1/3,273079) = 0,552741.
По этому же коэффициенту находим длины сторон треугольника АВС.
Площадь АВС = 7,1875 А1В1 = В1С1 = А1С1 = Р = 12,713046
AB =3,316447
BC =4,421929
AC =4,974670/
Площадь АВС находим по формуле Герона.
Р = 12,713046, р = 6,356523.
S(АВС) = 7,1875 кв.ед.
Проверяем соотношение длин сторон:
1 1,3333 1,5
1 4/3 3/2. Соответствует заданному.
ответ: площадь АВС = 7,1875 кв.ед.
ответ: √82 см
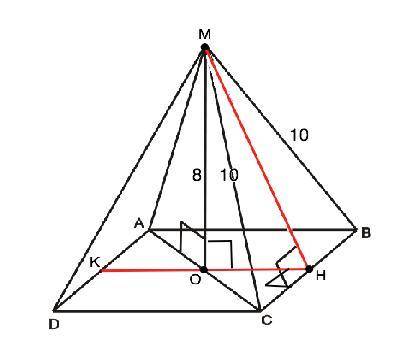
Объяснение: Вершина правильной четырехугольной пирамиды проецируется в центр основания - точку пересечения диагоналей квадрата. Пусть данная пирамида МАВСД, О - точка пересечения диагоналей основания. МО=8 - высота. МС=10 - боковое ребро, МН апофема ( высота боковой грани правильной пирамиды)
Из прямоугольного треугольника МОС по т.Пифагора половина диагонали ОС=√(МC²-МО²)=√(100-64)=6 см
Тогда по т. о 3-х перпендикулярах ОН⊥ВС. ⇒ ∆ ОНС - прямоугольный, ОН=ОС•sin45°=6•√2/2=3√2 ⇒
МН=√(МО²+ОН²)=√(64+18)=√82 см
Ну находим апофему, она равна 5 (по т. Пифагора). Находим площадь одной из 4 граней пирамиды, S=1/2 *a *h, S=15. Умножаем на 4, так как 4 грани, получаем 60.