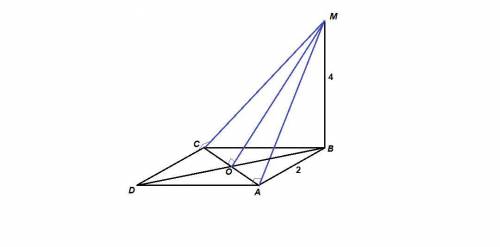
d(М, АВ) = d(M, BC) = 4 дм
d(M, AD) = d(M, СD) = 2√5 дм
d(M, BD) = 4 дм
d(M, AC) = 3√2 дм
Объяснение:
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к этой прямой.
МВ - перпендикуляр к плоскости квадрата, а значит, и к любой прямой, лежащей в этой плоскости.
МВ⊥АВ, значит расстояние от точки М до прямой АВ
d(М, АВ) = МВ = 4 дм
МВ⊥ВС, значит
d(M, BC) = MB = 4 дм
МВ⊥BD, значит
d(M, BD) = MB = 4 дм
BA⊥AD как стороны квадрата,
ВА - проекция МА на плоскость, значит МА⊥AD по теореме о трех перпендикулярах, тогда
d(M, AD) = MA
Аналогично, ВС⊥CD как стороны квадрата, ВС - проекция МС на плоскость, значит МС⊥CD по теореме о трех перпендикулярах, тогда
d(M, СD) = MС
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные:
ВС = ВА (стороны квадрата), значит МС = МА.
Из прямоугольного треугольника АВМ по теореме Пифагора:
МА = √(АВ² + ВМ²) = √(4 + 16) = √20 = 2√5 дм
Итак,
d(M, AD) = d(M, СD) = 2√5 дм
Осталось найти расстояние от М до диагонали АС.
ВО⊥АС по свойству диагоналей квадрата,
ВО - проекция МО на плоскость квадрата, значит
МО⊥АС по теореме о трех перпендикулярах.
d(M, AC) = MO
BD = AB√2 =2√2 дм как диагональ квадрата,
BО = BD/2 = √2 дм (диагонали квадрата делятся точкой пересечения пополам)
Из прямоугольного треугольника МВО по теореме Пифагора:
МО = √(ВО² + ВМ²) = √(2 + 16) = √18 = 3√2 дм
d(M, AC) = 3√2 дм
Дуга СD = 2 * ∠СBD = 2 * 27 = 54°
Дуга AD = 2 * ∠ACD = 2 * 54 = 108°
Дуга AB = 2 * ∠ADB = 2 * 62 = 124°
Дуга BC = 360 - (54 + 108 + 124) = 74°
∠АВС опирается на дугу ADC.
Дуга АDС = дуга АD + дуга СD = 108 + 54 = 162°
∠АВС = 162/2 = 81°
∠ВСD опирается на дугу ВAD.
Дуга ВАD = дуга АВ + дуга АD = 124 + 108 = 232°
∠ВСD = 232/2 = 116°
∠АDС опирается на дугу АВС.
Дуга АВС = дуга АВ + дуга ВС = 124 + 74 = 198°
∠АDС = 198/2 = 99°
Сумма углов четырехугольника = 360°, отсюда:
∠DАВ = 360 - (81 + 116 + 99) = 64°