Высота к гипотенузе делит прямоугольный треугольник на два, ему же - и между собой - подобные (это очень полезное заклинание, точно сильнее "авады кедавры").
Один из треугольников, НА которые высота разделила исходный треугольник, оказался Пифагоровым треугольником - раз у него одигн катет (это высота исходного тр-ка) 5, а гипотенуза (это катет исходного тр-ка) 13, то второй катет 12, и это один из отрезков, на которые высота делит гипотенузу. если обозначить второй отрезок x, то из подобия следует
x/5 = 5/12; x = 25/12;
Гипотенуза c равна c = 12 + 25/12 = 169/12;
Второй катет b можно найти так
b/13 = 5/12; b = 65/12;
На самом деле есть технический прием, который позволяет все это получить, так сказать, не думая.
Два треугольника со сторонами
(5, 12, 13)
(b, 13, c)
подобны друг другу, откуда
b = 5*13/12 = 65/12
c = 13*13/12 = 169/12
x = c - 12 = 25/12;
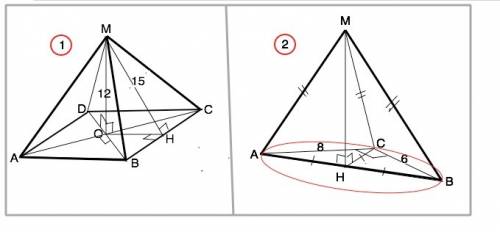
Обозначим пирамиду МАВСD, МО - высота, МН - апофема ( высота боковой грани).
Апофема делит сторону основания пополам. ВН=СН.
Диагонали квадрата пересекаются под прямым углом и при пересечении делятся пополам.
∆ ВОС в основании - прямоугольный равнобедренный.
МН⊥ВС. ⇒ по т. о 3-х перпендикулярах ОН ⊥ ВС, ⇒ ОН — высота и медиана ∆ ВОС. По свойству медианы ОН=BH=CH.
ОН=√(МН²-МО²)=√(225-144)=√81=9
BH=OH=9
MB=√(MH²+BH²)=√(225+81)=√306=3√34
№2
Если боковые ребра пирамиды равны, то равны и их проекции. Тогда проекции боковых ребер равны радиусу описанной около основания окружности. Для прямоугольного треугольника радиус описанной окружности равен половине гипотенузы ( значит, равен и медиане).
Гипотенуза прямоугольного треугольника с катетами 6 см и 8 см равна 10 см (египетский треугольник).
Тогда высота МН ( и медиана ) ∆ АМВ=АВ=10 см. ВН=АН=5 см
АМ= √(MH²+AH²)=√(100+25)=5√5 см
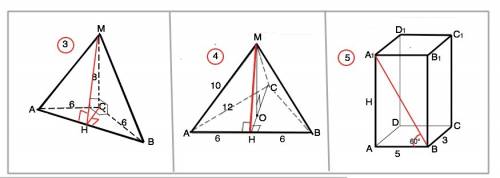
№3.
В основании пирамиды равнобедренный прямоугольный треугольник АВС, угол С=90°, АС=ВС=6 см. Высота пирамиды - третье из смежных ребер=8 см.
Площадь полной поверхности - сумма площади основания и площадей боковых граней.
S осн=АС•BC:2=18 см²
Грани АМС=ВМС по равенству катетов.
S ∆ AMC=S ∆ BMC=6•8:2=24 см²
S AMB=MH•AB:2
AB=AC:sin45°=6√2
CH высота и медиана ∆ АСВ=АВ:2=3√2
Высота MH большей боковой грани S=√(CH*+MH*)=√(18+64)=√82
S∆AMB=6√2•√82=6√164=12√41
S полн=18+2•24+12√41=(66+12√41) см²
№4
S полн=Sбок+Sосн
Боковые грани этой правильной пирамиды равны. Обозначим её МАВС.
МН- высота и медиана боковой грани. АН=ВН=6 см
∆ АМВ - равнобедренный. Апофема МН=√( АМ²-АН²)=√64=8 см
Sбок=3•МН•АВ:2=144 см²
Sосн=АВ²•√3:4=36√3 см²
Sполн=144+36√3=36(4+√3) см²
№5
Параллелепипед прямоугольный, следовательно, основание и боковые грани прямоугольники, а ребра перпендикулярны основанию и являются высотами параллелепипеда.
Обозначим большую сторону основания АВ, меньшую - ВС, высоту АА1.
Угол А1ВА=60° (дано)
А1А=АВ•tg60°=5√3
Площадь основания АВ•BC=5•3=15 Оснований два. S=2•15=30 см²
Площадь боковой пов-сти АА1•2(AB+BC)=5√3•16=80√3 см²
Sполн=(30+80√3) см²
l = sqrt(h^2 + R^2)
l = sqrt(64 + 36) = sqrt(100) = 10 см
Теперь найдем площадь боковой поверхности.
Sбок = ПRl
Sбок = 8 * 10 * П = 80П см^2
ответ: Sбок = 80П см^2.