Предисловие: всё что в вот таких скобках * * писать не надо, это комментарии, чтобы было понятно.
Рассматриваем треугольник АВС - прямоугольный *где уголА=90°, чтобы было понятно, что к чему, т. к. я пишу без рисунка*
Пусть уголС=60° (по условию).
УголС + уголВ = 90° (по свойству острых углов в пр-м тр-ке), следовательно
уголВ = 90° - уголС = 90° - 60° = 30°, значит (*катет*) АС = 1/2*ВС (*половине гипотенузы*) (по св-ву катета, лежащего против угла в 30°)
АС + ВС = 9 см (по условию)
Пусть ВС = х, тогда АС = 1/2*х. Имеем уравнение
х + 1/2*х = 9,
*превращаем х в неправильную дробь*
2\2*х + 1/2*х = 9,
3\2*х = 9,
х = 9 / 3/2 = *при делении переворачиваем дробь, получаем* 9*2/3 = 6
ВС = 6 (см)
ответ: ВС = 6 см.
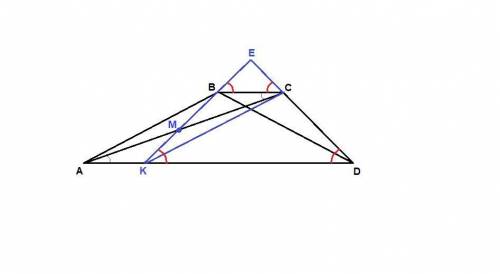
В трапеции ABCD боковая сторона AB равна диагонали BD. Точка M - середина диагонали AC. Прямая BM пересекает прямую CD в точке E. Докажите, что BE = CE.
Объяснение:
К - точка пересечения прямой ВМ с основанием AD.
Рассмотрим треугольники АМК и СМВ:
АМ = МС по условию,
∠АМК = ∠СМВ как вертикальные,
∠МАК = ∠МСВ как накрест лежащие при пересечении параллельных прямых АК и ВС секущей АС, ⇒
ΔАМК = ΔСМВ по стороне и двум прилежащим к ней углам.
Следовательно, АК = ВС.
Если в четырехугольнике две противолежащие стороны равны и параллельны, то это параллелограмм.
Значит, АВСК параллелограмм. ⇒ СК = АВ.
АВ = BD по условию, ⇒ СК = BD.
В трапеции KBCD диагонали равны, значит она равнобедренная.
Тогда ∠BKD = ∠CDK.
∠ЕВС = ∠BKD и ∠ЕСВ = ∠CDK как накрест лежащие при пересечении параллельных прямых KD и ВС секущими EК и ED соответственно, ⇒
∠EBC = ∠ECB.
Из этого следует, что треугольник ЕВС равнобедренный и
ВЕ = СЕ.
110, 110, 70, 70
Объяснение:
Тупой угол равен 20+90=110, так как высота перпендикулярна основаниям трапеции.
Так как трапеция равнобедренная, то углы при основании равны, второй угол при этом же основании равен 110.
Сумма противолежащих углов равносторонней трапеции равно 180, значит противолежащие углы равны 180-110=70.