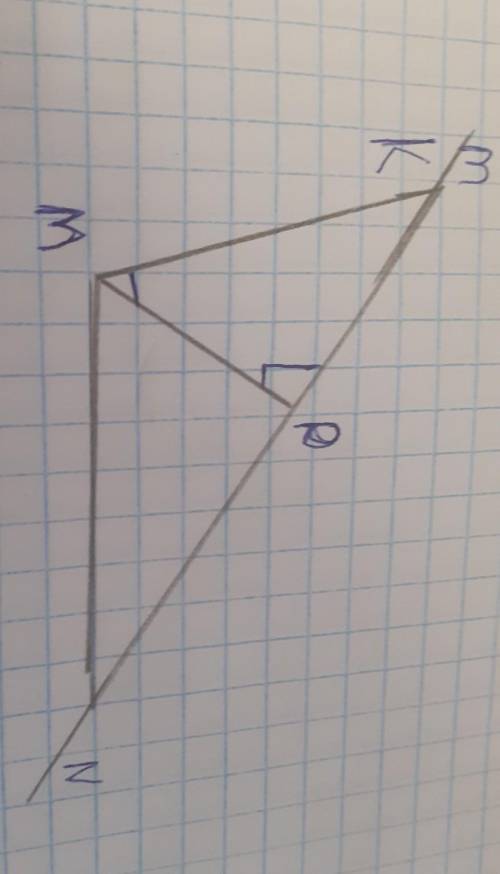
∠ 1 = ∠ 2 как накрест лежащие углы
Объяснение:
∠ BAC и ∠ DCA образованы при пересечении прямых AB и DC секущей AC. Поэтому ∠ BAC и ∠ DCA - это внутренние накрест лежащие углы.
Если накрест лежащие углы, образующиеся при пересечении двух
прямых секущей, равны, то прямые параллельны.
∠ BAC = ∠ DCA ⇒ AB || DC
∠ 1 и ∠ 2 образованы при пересечении прямых AB и DC секущей BD.
Поэтому ∠ 1 и ∠ 2 - это внутренние накрест лежащие углы.
Так как мы установили, что AB || DC, то ∠ 1 = ∠ 2 (Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны), что и требовалось доказать.
1- смежные углы в сумме дают 180 градусов, значит смежный угол с 30 градусами будет равен 150 градусам
смежный угол с 45 градусами будет равен 135 градусам т.к. 180-45=135
смежный угол с 60 градусами будет равен 120 градусам по той же схеме
и смежный угол с 90 градусам будет равен 90 градусам
Объяснение:
2 задание -
1) нет не могут. острые углы это углы которые меньше 90 градусов, а такие углы в сумме не смогут дать 180 градусов
2) не могут. тупые углы это углы, которые больше 90 градусов соответственно в сумме будет больше 180 градусов
3) да могут. прямые углы это углы равные 90 градусам. и в сумме они будут давать 180 градусов
--------------------
в фото в первом номере с 30 градусами точно также и с 45 и 60 градусами, только меняя сами числа( чертеж тот же)
сделала как смогла чертежи и объяснения.