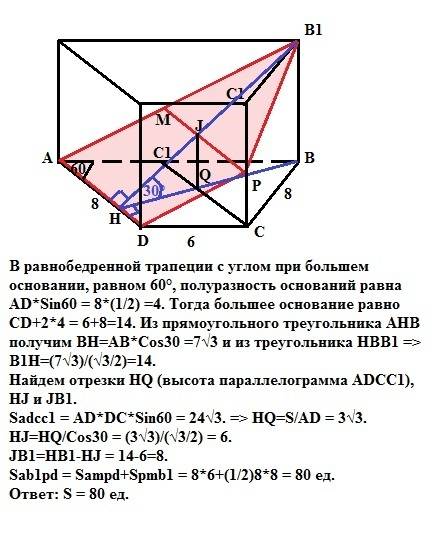
Для начала построим сечение призмы плоскостью АВ1D. Точки А и В1 принадлежат плоскости, содержащей грань АА1В1В, следовательно, линия пересечения этой грани плоскостью сечения пройдет по прямой АВ1. Зная, что две параллельные плоскости пересекаются третьей по параллельным линиям, проведем в грани DD1C1C из точки D прямую, параллельную прямой АВ1 до пересечения с ребром СС1 этой грани в точке Р. Соединив точки А,В1,Р, и D, получим искомое сечение АВ1РD.
Определение: Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Проведем перпендикуляр ВН в основании призмы (точка Н - пересечение его с ребром AD) и соединим точки В1 и Н прямой. По теореме о трех перпендикулярах В1Н перпендикулярна прямой AD. Следовательно, <B1HB является линейным углом двугранного угла между плоскостями сечения и основания призмы и равен 30° (дано). Проведем прямую РМ, параллельную прямой АВ.
Сечение призмы представляет собой четырехугольник, состоящий из параллелограмма АМРD и треугольника РМВ1.
Найдем высоту нашей трапеции, ее большее основание и длину перпендикуляра ВН.
В равнобедренной трапеции с углом при большем основании, равном 60°, полуразность оснований равна AD*Sin60 = 8*(1/2) =4. Тогда большее основание равно CD+2*4 = 6+8=14. Из прямоугольного треугольника АНВ получим ВН=АВ*Cos30 =7√3 и из треугольника НВВ1 => В1Н=(7√3)/(√3/2)=14.
Найдем отрезки HQ (высота параллелограмма ADCC1), HJ и JB1.
Sadcc1 = AD*DC*Sin60 = 24√3. => HQ=S/AD = 3√3.
HJ=HQ/Cos30 = (3√3)/(√3/2) = 6.
JB1=HB1-HJ = 14-6=8.
Sab1pd = Sampd+Spmb1 = 8*6+(1/2)8*8 = 80 ед.
ответ: S = 80 ед.
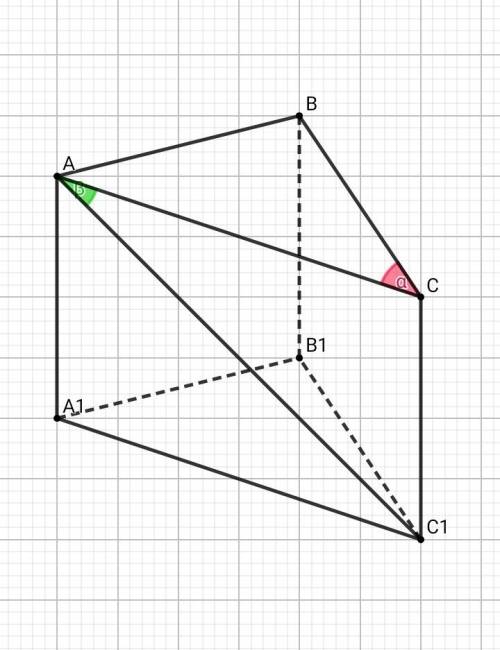
Продлим основание треугольника.
Опустим к нему высоту из вершины, лежащей против основания.
Эта высота противолежит углу 30° ( разность между развернутым углом и углом между сторонами треугольника)
Поэтому высота треугольника, опущенная из острого угла, равна половине стороны ( являющейся в этом прямоугольном треугольнике гипотенузой)
Имеется высота треугольника и основание, к которому она опущена.
На рисунке 1 в приложении гипотенузой получившегося прямоугольного треугольника стала сторона, равная 5 см.
Поэтому высота равна 5*sin(30°)=2,5 см
S=2,5*4:2=5 см²
С тем же результатом можно провести высоту к стороне, равной 5, и получим высоту, равную 2 см (см. рис.2)
S=2 *5:2=5 см²