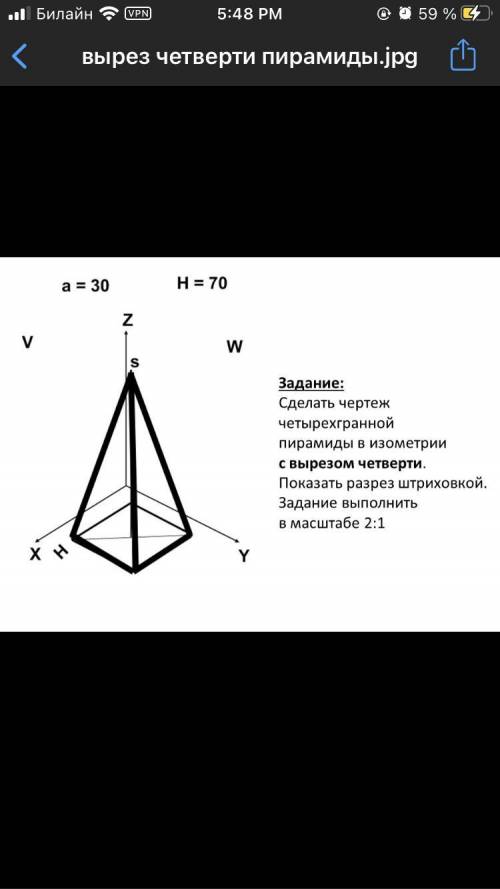
Каждое боковое ребро составляет с плоскостью основания угол в 45° - следовательно, все ребра равны, а их проекции равны радиусу описанной около основания пирамиды окружности, Основание высоты пирамиды - центр О описанной окружности. . Величина её радиуса АО равна 2/3 высоты основания.
AH=AB•sin60°=4√3/2=2√3
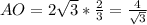
Высота МО перпендикулярна основанию
∆АМО - прямоугольный, острый угол МАО=45°, следовательно, второй АМО=45°, и высота пирамиды МО=АО=4/√3
Формула объёма пирамиды V=S•h:3
S(∆ABC)=AB²•√3/4=16√3/4=4√3
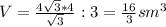
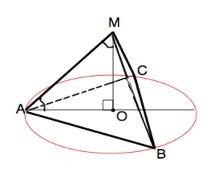
DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.