В прямом параллелепипеде стороны равны 3 см и 8 см, угол между ними 60°. Площадь боковой поверхности параллелепипеда 220 см². Найдите меньшую диагональ параллелепипеда.
* * *
На рисунке меньшая диагональ АС1 соединяет вершины тупых углов противоположных оснований.
Для решения требуется найти высоту СС1 и диагональ АС основания. S (бок)=Р•Н, где Р - периметр основания параллелепипеда, Н - его высота. ⇒ Н=220:2•(8+3)=10 см.
По т.косинусов АС²=ВС²+АВ²-2ВС•АС•cos60° ⇒ АС²=9+64 - 2•24•1/2 ⇒ АС²=49.
Из ⊿ АСС1 по т.Пифагора АС1=√(AC²+CC1²)=√(100+49)=√149 см, т.е. ≈12,2 см
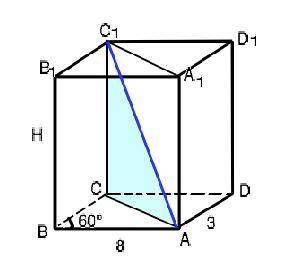
Сделаем рисунок.
Рассмотрим ∆ А1ОВ1.
Так как АВ и А1В1 расположены в параллельных плоскостях и лежат в плоскости ∆ А1ОВ1, АВ║А1В1.
⇒ соответственные углы этих треугольников образованные пересечением параллельных прямых и секущей равны, и
∆ АОВ~∆ A1OB1
На том же основании ВС║В1С1 и АС║А1С1⇒ ∆ АВС и ∆ А1В1С1 подобны.
Из подобия следует:
А1О:АО=14:10=k
k=1,4⇒
А1В1=2•1,4=2,8 см
B1C1=3•1,4=4,2 см
A1C1=4•1,4=5,6 см
Периметр ∆ А1В1С1=2,8+4,2+5,6=12,6 см