Грани правильного тетраэдра - равносторонние треугольники.
Их биссектриса является и высотой и медианой.
В сечении образуется равнобедренный треугольник, одна сторона которого равна ребру тетраэдра, две других - высоты грани.
Высота грани h = a*cos 30° = a√3/2 = 5√3/2.
Площадь сечения можно определить или 1) по формуле Герона, или 2) через высоту сечения.
1) Полупериметр p = 6,83013. Площадь S = √(p(p-a)(p-b)(p-c).
Поставив данные, получаем:
S = √( 6,83013*1,830123*2,5*2,5) = √78,125 = 8,83883.
2) Высота сечения из середины ребра на противоположное ребро равна:
h(c) = √(h² - (a/2)²) = √(18,75 - 6,25) = √12,5 ≈ 4,33013.
S = (1/2)*h(c)*a = (1/2)*5*4,330135 = 8,83883.
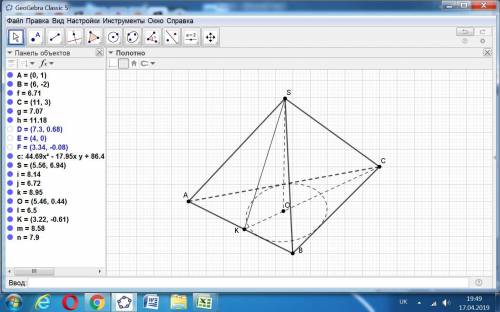
68. По данным на рисунке найдите площадь 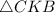 .
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :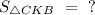 Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 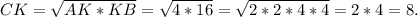
Следовательно, 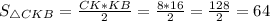 ед².
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите 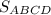 .
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :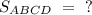
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 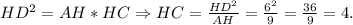
Следовательно, 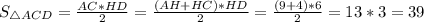 ед².
ед².
Тогда 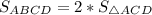 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
78 ед².
1.
наименьший угол - тот который лежит против меньшей стороны (9 см)
sin(a) = 9/41
cos(a) = 40/41
tg(a) = 9/40
ctg(a) = 40/9
2.
кос=катет:гипотенуза
отсюда следует что катет=косинус*гипотенузу=20*0,8=16(см)
по теореме Пифагора находим другой катет:
катет(второй) в кв=гипотенуза в кв - катет(первый)в кв=20 в кв - 16 в кв=400-256=144
катет(второй)=12(см)
3.
tg(a) = 2.5 / 2.5√(3) = 1 / √(3)
a = arctg(a) = arctg(1 / √(3)) = 30°
tg(B) = 2.5√(3) / 2.5 = √(3)
B = arctg(B) = arctg(√(3)) = 60°