1 задача расстояние от т О до MN назовем OQ
рассм. тр-к MOK и MOQ
- угол QMO = углу KOM (MS бисс)
- MO общая
- угол Q = угол K
тр-ки равны ⇒ OQ = OK = 9 см
Объяснение:
2 задача
A=60, <B=30, <C=90
Катет (меньший) -напротив угла в 30, он равен половине гипотенузы, то есть 1 часть +2 части=3 части
42:3=14 см-меньший катет
14*2=28 см-гипотенуза
3 задача
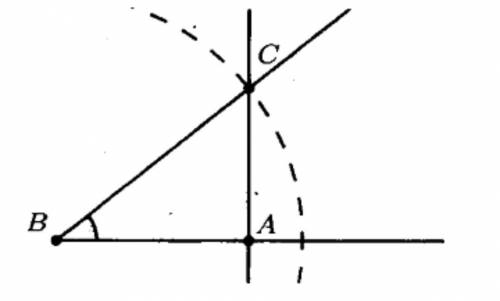
Строим острый угол В. Из вершины угла проводим окружность, радиусом равным длине гипотенузы. Так как треугольник — прямоугольный, то из точки пересечения окружности и угла С, опускаем перпендикуляр на противоположную сторону. В месте
пересечения перпендикуляра и стороны угла будет точка А. Попарно соединяем вершины треугольника. Искомый треугольник построен*. фото к 3 задаче
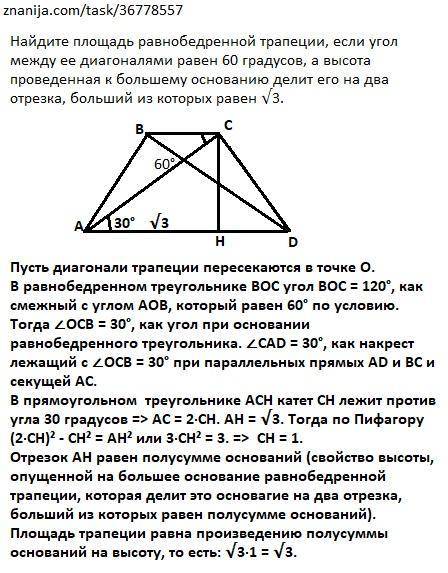
S = √3 ед².
Объяснение:
Пусть диагонали трапеции пересекаются в точке О.
В равнобедренном треугольнике ВОС угол ВОС = 120°, как смежный с углом АОВ, который равен 60° по условию. Тогда ∠ОСВ = 30°, как угол при основании равнобедренного треугольника. ∠CAD = 30°, как накрест лежащий с ∠ОСВ = 30° при параллельных прямых AD и ВС и секущей АС.
В прямоугольном треугольнике АСН катет СН лежит против угла 30 градусов => АС = 2·СН. АН = √3. Тогда по Пифагору
(2·СН)² - СН² = АН² или 3·СН² = 3. => СН = 1 ед.
Отрезок АН равен полусумме оснований (свойство высоты, опущенной на большее основание равнобедренной трапеции, которая делит это основание на два отрезка, больший из которых равен полусумме оснований). Итак, полусумма оснований равна √3 (дано). Тогда площадь трапеции равна произведению полусуммы оснований на высоту, то есть: √3·1 = √3 ед².
Найдем радиус:
S = ПR^2
289П = ПR^2
R = 17
d = 2R = 34
Найдем второй катет по теореме Пифагора:
B = sqrt(c^2 - a^2)
b = sqrt(1156 - 900) = sqrt(256) = 16
p = (a + b + c) * 1/2 = (30 + 34 + 16) * 1/2 = 40
S = ab/2 = 30 * 16/2 = 240
S = pr => r = S/p = 240/40 = 6
S = Пr^2 = 36П