Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=×AB =12÷2=6 см
DF || BC и EF=×BC=20÷2=10см
DE || AC; DE=×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см
Осевое сечение усеченного конуса - равнобедренная трапеция. основания: а=22 см (R₁*2), b=32 см (R₂*2) боковая сторона - образующая конуса l =13 см найти высоту равнобедренной трапеции - расстояние от центра верхнего основания до центра нижнего основания усеченного конуса перпендикуляры от верхнего основания до нижнего(из тупых углов) отсекают от равнобедренной трапеции 2 равных прямоугольных треугольника с гипотенузой(образующая конуса) 13 см и катетом 5 см ((32-22)/2=10/2=5 см). найти катет -H высоту усеченного конуса. по теореме Пифагора: 13²=5²+H². H²=169-25. H=12 cм ответ: расстояние между центрами оснований усеченного конуса 12 см
ответ: 1 сторона=6см
2сторона=10см
3 сторона 14см
Р=30см
Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=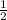 ×AB =12÷2=6 см
×AB =12÷2=6 см
DF || BC и EF=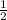 ×BC=20÷2=10см
×BC=20÷2=10см
DE || AC; DE=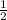 ×AC=28÷2=14см
×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см