Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 = 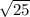 = 5
= 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3
1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.