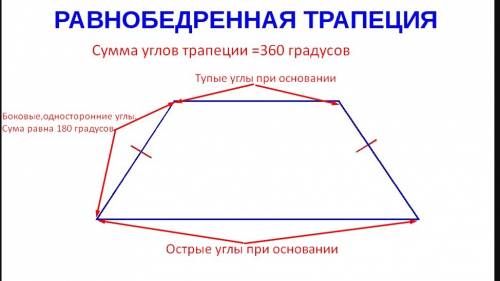
В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
°
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
Один угол равен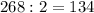 
°.
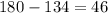°-из суммы боковых углов вычли тупой угол.
ответ:меньший угол трапеции равен 46 °.
(x+5)^2 + (y-3)^2=49;
Имеем уравнение (x-x0)^2 + (y-y0)^2=R^2; =>
x0=-5; y0=3, R=7;
x^2+25+10x+y^2+9-6y=49;
x^2+10x+y^2-6y+34-49=0;
- имеем общее уравнение окружности вида x^2 +y^2+A*x+B*y+C=0; A=10; B=-6;
Итак, центр окружности имеет координаты (-5;3), лежит он во 2-ой четверти (отрицательная ось кординат и положительная абсцисс), D=2R=2*7=14