|BC| = a = 2√3. |2AO+2CO| = 4. |AС - (3/2)*ОС| = 3.
Объяснение:
В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами.
АО - радиус описанной окружности. АО=ВО=СО= R = 2 см.
1. Из формулы радиуса описанной около правильного треугольника окружности R = √3*a/3 выразим сторону треугольника: а = R√3.
Тогда |BC| = a = 2√3.
2. При сложении векторов для нахождения длины суммы векторов используется теорема косинусов.
|2AO+2CO| = 2|AO+CO| = 2*√(AO²+CO² - 2AO*CO*Cosα').
α' - угол, смежный с углом между векторами.
В нашем случае угол между векторами АО и СО равен 120° (при свединении начал обоих векторов в одну точку). Следовательно, при вычислении длины вектора суммы векторов АО + СО, построенного по правилу треугольника, угол α' = 60° (смотри рисунок). Тогда
|2AO+2CO| = 2*√(4+4 - 2*2*2*1/2) = 4.
3. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус угла между векторами.
Угол между векторами АС и ОС в нашем случае равен 30°(смотри рисунок). Тогда
|AС - (3/2)*ОС| = √(12+(9/4)*4 - 2*2√3*2*√3/2) = 3.
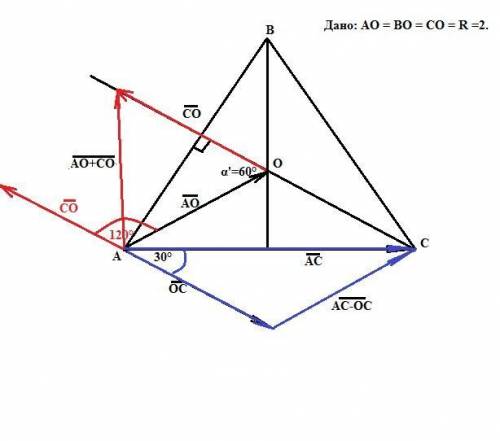
Чтобы понять геометрическую задачу, надо сделать правильный чертеж.
9 см, 4 см, 4 см.
Объяснение:
Дано: ΔАВС, АВ=ВС, ΔАСD; АС=СD=АD; Р(АВС)=17 см; Р(ADC)=27 см. Найти АВ, ВС, АС.
В равностороннем треугольнике все стороны равны, поэтому АС=СD=АD=27:3=9 см.
Рассмотрим ΔАВС, Р=17 см, АС=9 см, значит
АВ=ВС=(17-9):2=4 см.