OM делит AB пополам пересекая её. Так как части AB равны, то OM перпендикулярна AB. При этом продолжение OM пересекает и касательную, которая в свою очередь будет параллельна AB, т.к. она касается лишь одной точки и эта точка, точка пересечения OM.
Доказать это можно так:
OM перпендикулярна AB и касательной, значит образованные углы равны 90градусов, из этого следуют три признака док-ва параллельности:
-по на крест лежащим углам при AB, касательной и секущей OM
-по соответственным углам при AB, касательной и секущей OM
- по равносторонним углам при AB, касательной и секущей OM
Скорее всего вас в школе учили по-другому делать, но надеюсь хоть на мысль-то натолкнул:)
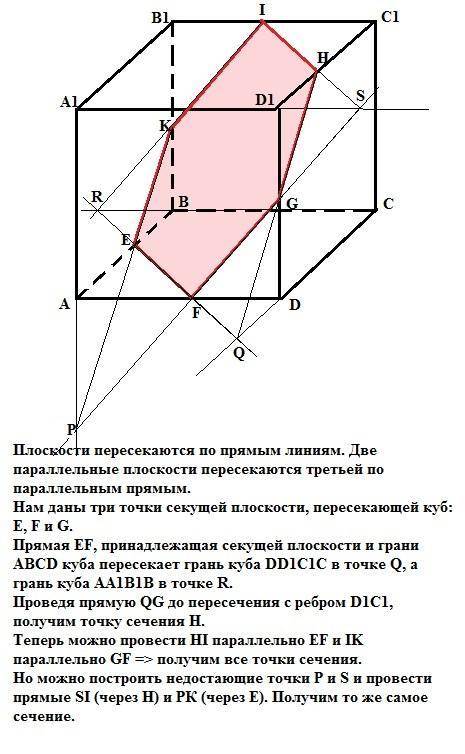
Сечение - правильный шестиугольник.
Объяснение:
Плоскости пересекаются по прямым линиям. Две параллельные плоскости пересекаются третьей по параллельным прямым.
Нам даны три точки секущей плоскости, пересекающей куб: E, F и G, расположенные на ребрах АВ, AD и DD1 соответственно.
Прямая EF, принадлежащая секущей плоскости и грани АВСD куба пересекает грань куба DD1C1C в точке Q, а грань куба AA1B1B в точке R.
Проведя прямую QG до пересечения с ребром D1C1, получим точку сечения Н.
Теперь можно провести НI параллельно EF и IK параллельно GF => получим все точки сечения.
Но можно построить недостающие точки P и S (построение понятно из рисунка) и провести прямые SI (через Н) и РК (через Е). Получим то же самое сечение, которое в силу симметричности точек является правильным шестиугольником.
решение на фото
можешь отметить мой ответ лучшим?)