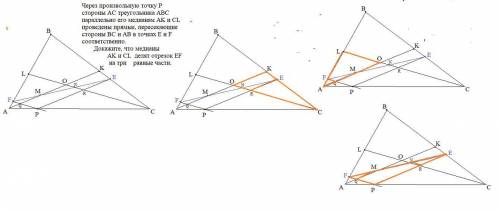
Через произвольную точку P стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.
Объяснение:
1) Медианы треугольника точкой пересечения делятся 2:1 , считая от вершины: ОК=1/3*АК ; LO=1/3*LC.
2)РЕ║АК ⇒ RE=1/3*PE,
PF║CL ⇒ QF=1/3*PE.
3)ΔREN подобен ΔPEF ( по 2 углам, там целая куча соответственных углов), значит сходственные стороны пропорциональны⇒
EN/EF=RE/PE или EN/EF=1/3 или EN=1/3*EF ;
ΔQFM подобен ΔPFE( по 2 углам) ,значит сходственные стороны пропорциональны⇒ FM/EF=QF/PE или FM/EF=1/3 или FM=1/3*EF.
4) Получили , что M и N разделили отрезок FE на 3 равные части.
Пусть A' – середина дуги BC. Так как OA' || IA2, прямые OI и A'A2 пересекаются в точке K – центре гомотетии описанной и вписанной окружностей (см. рис.). Докажем, что K – искомый радикальный центр.
Первый Так как инверсия с центром A' и радиусом A'B меняет местами прямую BC и описанную окружность Ω треугольника ABC, точка A1 переходит в A, а A2 – в точку A'' пересечения прямой A'A2 с описанной окружностью. Следовательно, точки A, A1, A2 и A'' лежат на одной окружности.
Степень точки K относительно описанной окружности треугольника AA1A2 равна – KA2·KA'' = – r/R AA'·KA'' = r/R s(K), где s(K) – степень точки K относительно Ω.
Очевидно, степени точки K относительно описанных окружностей треугольников BB1B2 и CC1C2 будут такими же, то есть K – радикальный центр трёх окружностей.
Второй Пусть A', B', C' – середины дуг BC, CA, AB. Тогда треугольник A'B'C' переводится в A2B2C2 гомотетией с коэффициентом r/R и центром K, то есть KA2 : A'A2 = KB2 : B'B2 = KC2 : C'C2 = k : 1. Для точек прямой A'A2 разность степеней относительно описанной окружности треугольника AA1A2 и вписанной окружности треугольника ABC является линейной функцией. В точке A2 эта функция равна нулю,
а в точке A' – r², поскольку A'A1·A'A = A'B² = A'I² (первое равенсто следует из подобия треугольников A'A1B и A'BA, а второе – из леммы о трезубце – см. задачу 53119). Значит, в точке K эта разность равна – kr². Другие аналогичные разности в точке K также равны – kr², откуда и следует требуемое