ответ: 1878,25см²
Объяснение:
1. В трапеции сумма углов, прилегающих к одной стороне равна 180° Угол при нижнем основании трапеции равен:
180-135=45°
2. Высота, проведенная из вершины угла 135° разделила этот угол на 90° и 135-95=45°.
3. Получили равнобедренный прямоугольный треугольник, один катет которого равен 2,75дм. Значит и второй катет равен 2,75дм. А второй катет является высотой трапеции.
4. Высота разделила нижнее основание на отрезки. Значит длина нижнего основания равна:
27,5+68,3=95,8см
5. Верхнее основание равно разности отрезков нижнего основания, разделенных высотой:
68,3-27,5=40,8см
6. Площадь трапеции равна: половине суммы оснований умноженной на высоту:
S=(40,8+95,8)/2*27,5=1878,25см²
ответ: 18° ( возможно Вы ошиблись записывая ответы? и в ответе Е 18 °)
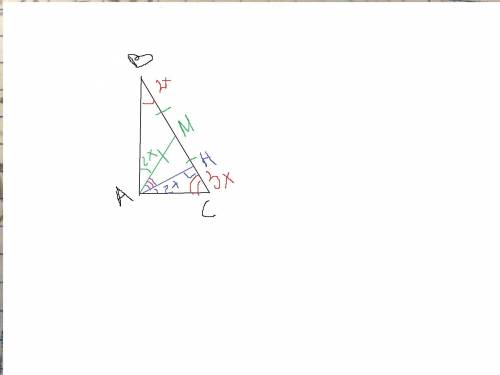
Дано: ΔАВС, ∠А=90°,∠А:∠В=2:3, АМ- медиана, АН- высота
Найти: ∠МАН-?
Пусть ∠В=2х, ∠С=3х, тогда по теореме о сумме острых углов треугольника:
2х+3х=90°;
5х=90°;
х=90°:5;
х=18°.
∠В=2*18°=36°
∠С=3*18°=54°.
Рассмотрим ΔАНС, где ∠Н=90°, ∠С=54°, следовательно
∠НАС=90°-54°=36°.
Так как АМ- медиана, то вокруг треугольника АВС можно описать окружность с центром в точке М и по свойству медианы, проведённой из прямого угла к гипотенузе она равна половине гипотенузы. То есть АМ=ВМ=СМ.
Рассмотрим ΔАВМ, так как АМ=ВМ, то треугольник равнобедренный, следовательно ∠В=∠АВМ=36° как углы при основании равнобедренного треугольника.
∠МАН=∠А-∠АВМ-НАС=90°-36°-36°=18°
Вообще-то, центром вписанной окружности является точка пересечения биссектрис внутренних углов треугольника