От квадрата со стороной a отсечены:
треугольник, равный 1/8 площади квадрата
два симметричных треугольника с катетами a и a*tg15
Искомая площадь равна
S= a^2(1 -1/8 -tg15) =a^2(8√3 -9)/8
R - радиус описанной окружности
Сторона квадрата a =R√2
Сторона треугольника 12 =R√3
a= 12*√2/√3 =4√6
S= 12(8√3 -9) =96√3 -108
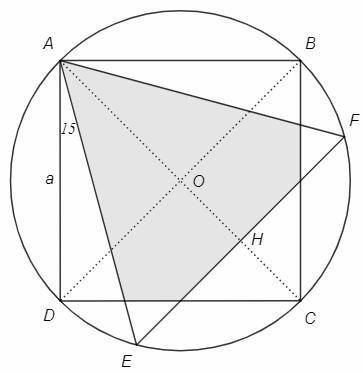
Центр окружности - на пересечении диагоналей квадрата. Треугольник имеет с квадратом общую вершину, следовательно серединный перпендикуляр к основанию совпадает с диагональю квадрата.
AO/OH =2/1 (AH - медиана), AO=OC (радиусы) => OC/OH =2/1.
BD⊥AC, EF⊥AC => BD||EF. По теореме Фалеса EF делит стороны BC и CD в том же отношении, что и OC, то есть пополам.
DAE= (DAB-EAF)/2 =(90-60)/2 =15
tg15 =tg(30/2) =(1-cos30)/sin30 =2(1-√3/2) =2-√3
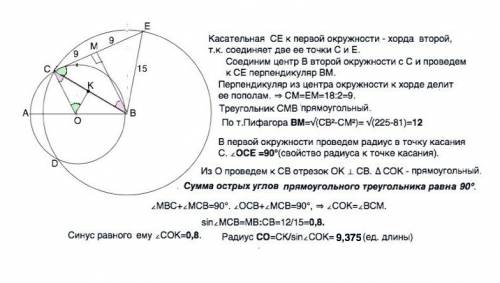
Касательная СЕ к первой окружности - хорда второй, т.к. соединяет две ее точки С и Е.
Соединим центр В второй окружности с С и проведем к СЕ перпендикуляр ВМ.
Перпендикуляр из центра окружности к хорде делит ее пополам. ⇒ СМ=ЕМ=18:2=9. Треугольник СМВ прямоугольный.
По т.Пифагора ВМ=√(СВ²-СМ²)= √(225-81)=12
В первой окружности проведем радиус в точку касания С. ∠ОСЕ =90°(свойство радиуса к точке касания).
Из О проведем к СВ отрезок ОК ⊥ СВ. ∆ СОК - прямоугольный. Сумма острых углов прямоугольного треугольника равны 90°.
∠МВС+∠МСВ=90°. ∠ОСВ+∠МСВ=90°, ⇒ ∠СОК=∠ВСМ. sin∠МСВ=МВ:СВ=12/15=0,8. Синус равного ему ∠СОК=0,8.
Радиус СО=СК/sin∠COK= 9,375 (ед. длины)
Vкуба=a³
Vшара=4PR³/3
R=a/2
Vшара=4Pa³/8*3 = Pa³/6=a³*0,52
Обьем вписанного шара это 52% от обьема куба.
Значит,52% сточили.
ответ:52%