Доказать равенство отрезков по представленному рисунку.
Доказательство:
Докажем, что AO = OC, исходя из признаков равенства треугольников.
1) Рассмотрим треугольники BCD и BAD.
BC = BA по условию (отмечено на рисунке);
CD = AD по условию (отмечено на рисунке);
BD - общая сторона.
Третий признак равенства: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
ΔBCD = ΔBAD по третьему признаку (по трем сторонам).
2) В равных треугольниках соответствующие углы равны, соответствующие стороны равны.
Следовательно ∠CBD = ∠ABD, а значит ∠CBO = ∠ABO.
3) Рассмотрим треугольники CBO и BAO.
BC = BA по условию;
BO общая сторона;
∠CBO = ∠ABO из равенства треугольников BCD и BAD (см п.2).
Первый признак равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
ΔCBO = ΔBAO по первому признаку (по двум сторонам и углу между ними).
4) Так как в равных треугольниках соответствующие стороны равны, то АО=ОС.
Доказано.
ответ: 1. Знайдемо координати точки М, яка є серединою сторони АС за формулою ділення відрізка на дві рівні частини:
Хм=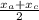
= 
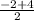=1; Yм=
=
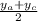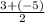= -1
Отже, координати точки М (1;-1).
2. Довжину медиани знайдемо, як відстань між двома точками за формулою:
BM =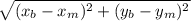
=
= 
одиниць.
3. Рівняння медиани ВМ запишемо, скориставшисьформулою рівняння прямої, щопроходить через дві точки:
Підставивши координати точок В(0;1) і М(1;-1) запишемо загальне рівняння медиани ВМ:
х=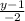
;
-2х=у-1;
-2х-у+1=0.
Для знаходження рівняння з кутовим коефіцієнтом kВМ медиани ВМ, розв"яжемоотримане рівняння відносно у:
у= -2х+1, звідси k=-2.
Відповідь: довжина медиани
одиниць, загальне рівняння медиани -2х-у+1=0, рівняння з кутовим коефіцієнтом у=-2х+1.
Малюнок до задачі в додатку.
Объяснение: